Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 15570 by tawa tawa last updated on 11/Jun/17

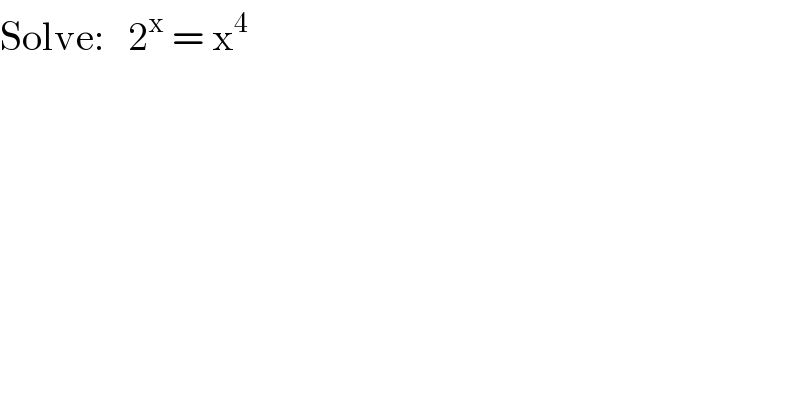
Solve: 2^x = x^4

$$\mathrm{Solve}:\:\:\:\mathrm{2}^{\mathrm{x}} \:=\:\mathrm{x}^{\mathrm{4}} \\ $$

Commented by tawa tawa last updated on 11/Jun/17

workings

$$\mathrm{workings} \\ $$

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 12/Jun/17

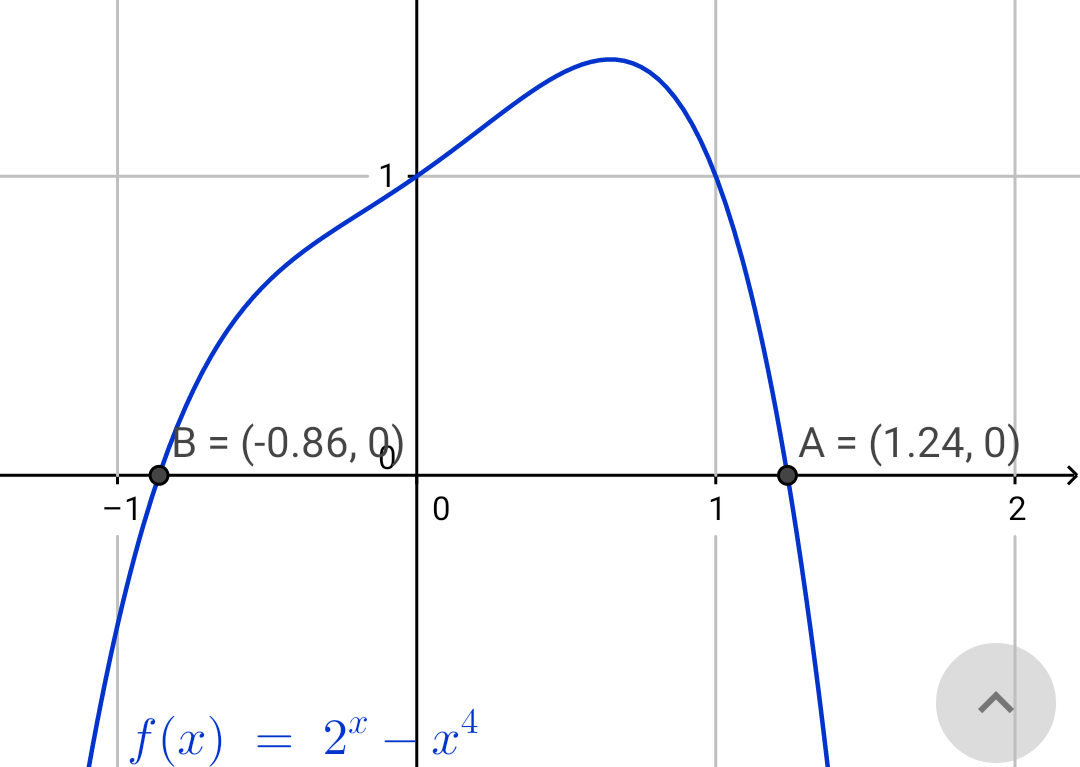
Commented by mrW1 last updated on 12/Jun/17

the graph is much bigger than what you display. there is a third zero point on the right side.

$$\mathrm{the}\:\mathrm{graph}\:\mathrm{is}\:\mathrm{much}\:\mathrm{bigger}\:\mathrm{than}\:\mathrm{what} \\ $$$$\mathrm{you}\:\mathrm{display}.\:\mathrm{there}\:\mathrm{is}\:\mathrm{a}\:\mathrm{third}\:\mathrm{zero} \\ $$$$\mathrm{point}\:\mathrm{on}\:\mathrm{the}\:\mathrm{right}\:\mathrm{side}. \\ $$

Commented by tawa tawa last updated on 12/Jun/17

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$ \\ $$

Answered by mrW1 last updated on 12/Jun/17

2^x =x^4 2^(x/4) =±x e^((x/4)ln 2) =±x ±1=xe^(−((xln 2)/4)) ∓((ln 2)/4)=(−((xln 2)/4))e^((−((xln 2)/4))) ⇒−((xln 2)/4)=W(∓((ln 2)/4)) x=((W(∓((ln 2)/4)))/(−((ln 2)/4)))=((W(∓0.173287))/(−0.173287)) = { ((((−2.772589)/(−0.173287))=16)),((((−0.214811)/(−0.173287))=1.2396)),((((0.149260)/(−0.173287))=−0.8613)) :}

$$\mathrm{2}^{\mathrm{x}} =\mathrm{x}^{\mathrm{4}} \\ $$$$\mathrm{2}^{\frac{\mathrm{x}}{\mathrm{4}}} =\pm\mathrm{x} \\ $$$$\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{4}}\mathrm{ln}\:\mathrm{2}} =\pm\mathrm{x} \\ $$$$\pm\mathrm{1}=\mathrm{xe}^{−\frac{\mathrm{xln}\:\mathrm{2}}{\mathrm{4}}} \\ $$$$\mp\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}=\left(−\frac{\mathrm{xln}\:\mathrm{2}}{\mathrm{4}}\right)\mathrm{e}^{\left(−\frac{\mathrm{xln}\:\mathrm{2}}{\mathrm{4}}\right)} \\ $$$$\Rightarrow−\frac{\mathrm{xln}\:\mathrm{2}}{\mathrm{4}}=\mathrm{W}\left(\mp\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}\right) \\ $$$$\mathrm{x}=\frac{\mathrm{W}\left(\mp\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}\right)}{−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}}=\frac{\mathrm{W}\left(\mp\mathrm{0}.\mathrm{173287}\right)}{−\mathrm{0}.\mathrm{173287}} \\ $$$$=\begin{cases}{\frac{−\mathrm{2}.\mathrm{772589}}{−\mathrm{0}.\mathrm{173287}}=\mathrm{16}}\\{\frac{−\mathrm{0}.\mathrm{214811}}{−\mathrm{0}.\mathrm{173287}}=\mathrm{1}.\mathrm{2396}}\\{\frac{\mathrm{0}.\mathrm{149260}}{−\mathrm{0}.\mathrm{173287}}=−\mathrm{0}.\mathrm{8613}}\end{cases} \\ $$

Commented by tawa tawa last updated on 12/Jun/17

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$ \\ $$

Commented by Tinkutara last updated on 12/Jun/17

Sir, how do you calculate W(± 0.173287)? Is there any method to calculate this without calculator? How to find this using Geogebra?

$$\mathrm{Sir},\:\mathrm{how}\:\mathrm{do}\:\mathrm{you}\:\mathrm{calculate}\:{W}\left(\pm\:\mathrm{0}.\mathrm{173287}\right)? \\ $$$$\mathrm{Is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{method}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{this} \\ $$$$\mathrm{without}\:\mathrm{calculator}?\:\mathrm{How}\:\mathrm{to}\:\mathrm{find}\:\mathrm{this} \\ $$$$\mathrm{using}\:\mathrm{Geogebra}? \\ $$

Commented by mrW1 last updated on 12/Jun/17

Normal calculators don′t have this Lambert function. There are some online calculators for W−function, but most of them give only one value for x<0. With geogebra you can calculate W−function value by yourself: For example you want to calculate W(−((ln 2)/4)). That is the root(s) of f(x)=xe^x +((ln 2)/4).

$$\mathrm{Normal}\:\mathrm{calculators}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{this} \\ $$$$\mathrm{Lambert}\:\mathrm{function}.\:\mathrm{There}\:\mathrm{are}\:\mathrm{some} \\ $$$$\mathrm{online}\:\mathrm{calculators}\:\mathrm{for}\:\mathrm{W}−\mathrm{function}, \\ $$$$\mathrm{but}\:\mathrm{most}\:\mathrm{of}\:\mathrm{them}\:\mathrm{give}\:\mathrm{only}\:\mathrm{one}\:\mathrm{value} \\ $$$$\mathrm{for}\:\mathrm{x}<\mathrm{0}. \\ $$$$\mathrm{With}\:\mathrm{geogebra}\:\mathrm{you}\:\mathrm{can}\:\mathrm{calculate} \\ $$$$\mathrm{W}−\mathrm{function}\:\mathrm{value}\:\mathrm{by}\:\mathrm{yourself}: \\ $$$$\mathrm{For}\:\mathrm{example}\:\mathrm{you}\:\mathrm{want}\:\mathrm{to}\:\mathrm{calculate} \\ $$$$\mathrm{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}\right).\:\mathrm{That}\:\mathrm{is}\:\mathrm{the}\:\mathrm{root}\left(\mathrm{s}\right)\:\mathrm{of} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{xe}^{\mathrm{x}} +\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}. \\ $$

Commented by mrW1 last updated on 12/Jun/17

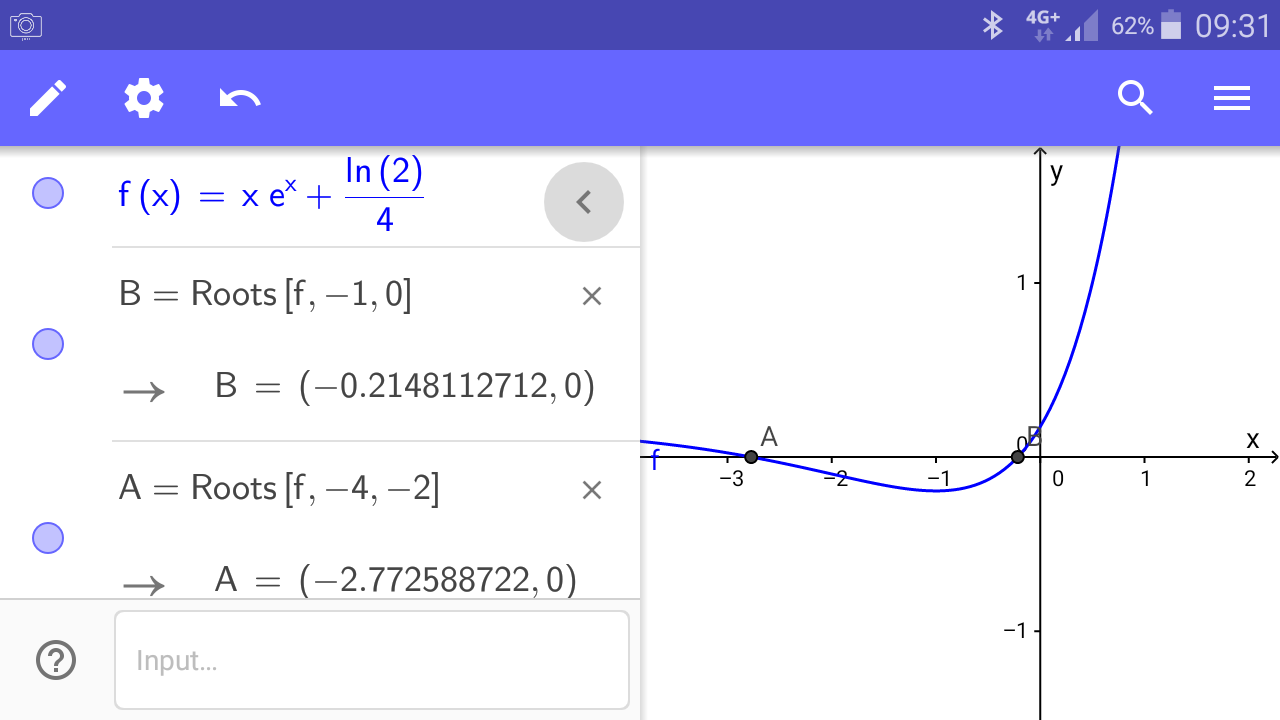
Commented by Tinkutara last updated on 12/Jun/17

Do you mean that in general if we want W(n), these are the roots of f(x) = xe^x − n ?

$$\mathrm{Do}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{that}\:\mathrm{in}\:\mathrm{general}\:\mathrm{if}\:\mathrm{we} \\ $$$$\mathrm{want}\:{W}\left({n}\right),\:\mathrm{these}\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of} \\ $$$${f}\left({x}\right)\:=\:{xe}^{{x}} \:−\:{n}\:? \\ $$

Commented by mrW1 last updated on 12/Jun/17

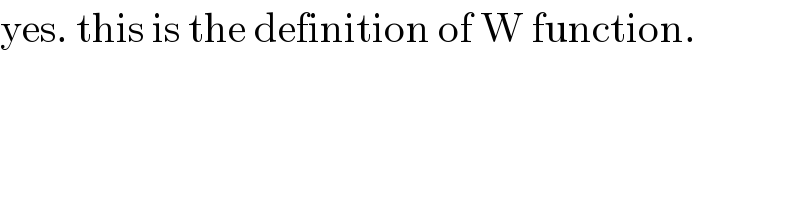
yes. this is the definition of W function.

$$\mathrm{yes}.\:\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{definition}\:\mathrm{of}\:\mathrm{W}\:\mathrm{function}. \\ $$

Commented by Tinkutara last updated on 12/Jun/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Commented by tawa tawa last updated on 12/Jun/17

logx^6 = (x/6) 6logx = x/6 36logx = x x^(36) = e^x 1 = x^(36) e^(−x) log .... Sir, i have been thinking. i have a question. What is my aim in solving using lambert function. Please give example as the number 1, i will use it to solve number 2. my problem here is that i dont even have starting point. Thank you sir. I want to learn it. The starting point is my problem. please do number 1 as example.

$$\mathrm{logx}^{\mathrm{6}} \:=\:\frac{\mathrm{x}}{\mathrm{6}} \\ $$$$\mathrm{6logx}\:=\:\mathrm{x}/\mathrm{6} \\ $$$$\mathrm{36logx}\:=\:\mathrm{x} \\ $$$$\mathrm{x}^{\mathrm{36}} \:=\:\mathrm{e}^{\mathrm{x}} \\ $$$$\mathrm{1}\:=\:\mathrm{x}^{\mathrm{36}} \:\mathrm{e}^{−\mathrm{x}} \\ $$$$\mathrm{log}\:.... \\ $$$$\mathrm{Sir},\:\mathrm{i}\:\mathrm{have}\:\mathrm{been}\:\mathrm{thinking}. \\ $$$$\mathrm{i}\:\mathrm{have}\:\mathrm{a}\:\mathrm{question}.\: \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{my}\:\mathrm{aim}\:\mathrm{in}\:\mathrm{solving}\:\mathrm{using}\:\mathrm{lambert}\:\mathrm{function}. \\ $$$$\mathrm{Please}\:\mathrm{give}\:\mathrm{example}\:\mathrm{as}\:\mathrm{the}\:\mathrm{number}\:\mathrm{1},\:\mathrm{i}\:\mathrm{will}\:\mathrm{use}\:\mathrm{it}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{number}\:\mathrm{2}. \\ $$$$\mathrm{my}\:\mathrm{problem}\:\mathrm{here}\:\mathrm{is}\:\mathrm{that}\:\mathrm{i}\:\mathrm{dont}\:\mathrm{even}\:\mathrm{have}\:\mathrm{starting}\:\mathrm{point}. \\ $$$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{learn}\:\mathrm{it}. \\ $$$$\mathrm{The}\:\mathrm{starting}\:\mathrm{point}\:\mathrm{is}\:\mathrm{my}\:\mathrm{problem}.\: \\ $$$$\mathrm{please}\:\mathrm{do}\:\mathrm{number}\:\mathrm{1}\:\mathrm{as}\:\mathrm{example}. \\ $$

Commented by tawa tawa last updated on 12/Jun/17

Please give me one question on this, let me solve it.

$$\mathrm{Please}\:\mathrm{give}\:\mathrm{me}\:\mathrm{one}\:\mathrm{question}\:\mathrm{on}\:\mathrm{this},\:\mathrm{let}\:\mathrm{me}\:\mathrm{solve}\:\mathrm{it}. \\ $$

Commented by mrW1 last updated on 12/Jun/17

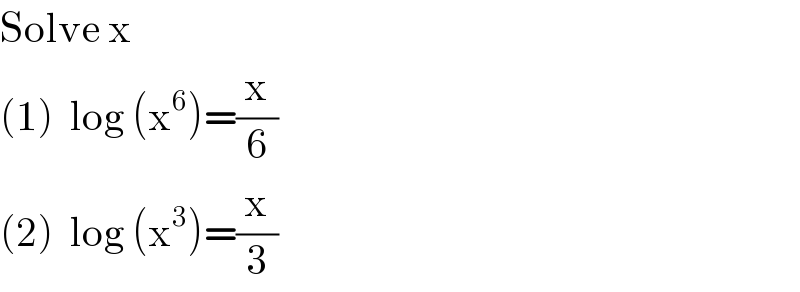
Solve x (1) log (x^6 )=(x/6) (2) log (x^3 )=(x/3)

$$\mathrm{Solve}\:\mathrm{x} \\ $$$$\left(\mathrm{1}\right)\:\:\mathrm{log}\:\left(\mathrm{x}^{\mathrm{6}} \right)=\frac{\mathrm{x}}{\mathrm{6}} \\ $$$$\left(\mathrm{2}\right)\:\:\mathrm{log}\:\left(\mathrm{x}^{\mathrm{3}} \right)=\frac{\mathrm{x}}{\mathrm{3}} \\ $$

Commented by mrW1 last updated on 12/Jun/17

To be able to use Lambert function we must re−arange the original equation into following form: A×e^A =B wherein A is a expression with x and B is a expression with constants only. The solution is then A=W(B) Example 1: log x^6 =(x/6) ⇒6log (±x)=(x/6) (± because x can be + or −) we consider +x at first ⇒log (x)=(x/(36)) ⇒((ln x)/(ln 10))=(x/(36)) ⇒ln x=((ln 10)/(36))x ⇒x=e^((ln 10 x)/(36)) ⇒xe^(−((ln 10 x)/(36))) =1 ⇒(−((ln 10 x)/(36)))e^(−((ln 10 x)/(36)) ) =−((ln 10)/(36)) this is the form A×e^A =B we need. the solution is −((ln 10 x)/(36))=W(−((ln 10)/(36))) ⇒x=−((36)/(ln 10))×W(−((ln 10)/(36))) we will get here 2 values for x, since W(−((ln 10)/(36))) has 2 values. similarly for the case −x we have ⇒log (−x)=(x/(36)) ⇒((ln (−x))/(ln 10))=(x/(36)) ⇒ln (−x)=((ln 10)/(36))x ⇒−x=e^((ln 10 x)/(36)) ⇒−xe^(−((ln 10 x)/(36))) =1 ⇒(−((ln 10 x)/(36)))e^(−((ln 10 x)/(36)) ) =((ln 10)/(36)) ⇒−((ln 10 x)/(36))=W(((ln 10)/(36))) ⇒x=−((36)/(ln 10))×W(((ln 10)/(36))) we will get here only one value for x. All solutions are thus x= { ((−((36)/(ln 10))×W(−((ln 10)/(36))) → 2 values)),((−((36)/(ln 10))×W(((ln 10)/(36))) → 1 value)) :}

$$\mathrm{To}\:\mathrm{be}\:\mathrm{able}\:\mathrm{to}\:\mathrm{use}\:\mathrm{Lambert}\:\mathrm{function} \\ $$$$\mathrm{we}\:\mathrm{must}\:\mathrm{re}−\mathrm{arange}\:\mathrm{the}\:\mathrm{original} \\ $$$$\mathrm{equation}\:\mathrm{into}\:\mathrm{following}\:\mathrm{form}: \\ $$$$\mathrm{A}×\mathrm{e}^{\mathrm{A}} =\mathrm{B} \\ $$$$\mathrm{wherein}\:\mathrm{A}\:\mathrm{is}\:\mathrm{a}\:\mathrm{expression}\:\mathrm{with}\:\mathrm{x}\:\mathrm{and} \\ $$$$\mathrm{B}\:\mathrm{is}\:\mathrm{a}\:\mathrm{expression}\:\mathrm{with}\:\mathrm{constants}\:\mathrm{only}. \\ $$$$\mathrm{The}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{then} \\ $$$$\mathrm{A}=\boldsymbol{\mathrm{W}}\left(\mathrm{B}\right) \\ $$$$\mathrm{Example}\:\mathrm{1}:\:\mathrm{log}\:\mathrm{x}^{\mathrm{6}} =\frac{\mathrm{x}}{\mathrm{6}} \\ $$$$\Rightarrow\mathrm{6log}\:\left(\pm\mathrm{x}\right)=\frac{\mathrm{x}}{\mathrm{6}}\:\:\:\:\:\:\:\:\:\:\left(\pm\:\mathrm{because}\:\mathrm{x}\:\mathrm{can}\:\mathrm{be}\:+\:\mathrm{or}\:−\right) \\ $$$$\mathrm{we}\:\mathrm{consider}\:+\mathrm{x}\:\mathrm{at}\:\mathrm{first} \\ $$$$\Rightarrow\mathrm{log}\:\left(\mathrm{x}\right)=\frac{\mathrm{x}}{\mathrm{36}} \\ $$$$\Rightarrow\frac{\mathrm{ln}\:\mathrm{x}}{\mathrm{ln}\:\mathrm{10}}=\frac{\mathrm{x}}{\mathrm{36}} \\ $$$$\Rightarrow\mathrm{ln}\:\mathrm{x}=\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{36}}\mathrm{x} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{e}^{\frac{\mathrm{ln}\:\mathrm{10}\:\mathrm{x}}{\mathrm{36}}} \\ $$$$\Rightarrow\mathrm{xe}^{−\frac{\mathrm{ln}\:\mathrm{10}\:\mathrm{x}}{\mathrm{36}}} =\mathrm{1} \\ $$$$\Rightarrow\left(−\frac{\mathrm{ln}\:\mathrm{10}\:\mathrm{x}}{\mathrm{36}}\right)\mathrm{e}^{−\frac{\mathrm{ln}\:\mathrm{10}\:\mathrm{x}}{\mathrm{36}}\:} =−\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{36}} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{form}\:\mathrm{A}×\mathrm{e}^{\mathrm{A}} =\mathrm{B}\:\mathrm{we}\:\mathrm{need}. \\ $$$$\mathrm{the}\:\mathrm{solution}\:\mathrm{is} \\ $$$$−\frac{\mathrm{ln}\:\mathrm{10}\:\mathrm{x}}{\mathrm{36}}=\boldsymbol{\mathrm{W}}\left(−\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{36}}\right) \\ $$$$\Rightarrow\mathrm{x}=−\frac{\mathrm{36}}{\mathrm{ln}\:\mathrm{10}}×\boldsymbol{\mathrm{W}}\left(−\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{36}}\right) \\ $$$$\mathrm{we}\:\mathrm{will}\:\mathrm{get}\:\mathrm{here}\:\mathrm{2}\:\mathrm{values}\:\mathrm{for}\:\mathrm{x},\:\mathrm{since} \\ $$$$\boldsymbol{\mathrm{W}}\left(−\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{36}}\right)\:\mathrm{has}\:\mathrm{2}\:\mathrm{values}. \\ $$$$ \\ $$$$\mathrm{similarly}\:\mathrm{for}\:\mathrm{the}\:\mathrm{case}\:−\mathrm{x}\:\mathrm{we}\:\mathrm{have} \\ $$$$\Rightarrow\mathrm{log}\:\left(−\mathrm{x}\right)=\frac{\mathrm{x}}{\mathrm{36}} \\ $$$$\Rightarrow\frac{\mathrm{ln}\:\left(−\mathrm{x}\right)}{\mathrm{ln}\:\mathrm{10}}=\frac{\mathrm{x}}{\mathrm{36}} \\ $$$$\Rightarrow\mathrm{ln}\:\left(−\mathrm{x}\right)=\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{36}}\mathrm{x} \\ $$$$\Rightarrow−\mathrm{x}=\mathrm{e}^{\frac{\mathrm{ln}\:\mathrm{10}\:\mathrm{x}}{\mathrm{36}}} \\ $$$$\Rightarrow−\mathrm{xe}^{−\frac{\mathrm{ln}\:\mathrm{10}\:\mathrm{x}}{\mathrm{36}}} =\mathrm{1} \\ $$$$\Rightarrow\left(−\frac{\mathrm{ln}\:\mathrm{10}\:\mathrm{x}}{\mathrm{36}}\right)\mathrm{e}^{−\frac{\mathrm{ln}\:\mathrm{10}\:\mathrm{x}}{\mathrm{36}}\:} =\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{36}} \\ $$$$\Rightarrow−\frac{\mathrm{ln}\:\mathrm{10}\:\mathrm{x}}{\mathrm{36}}=\boldsymbol{\mathrm{W}}\left(\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{36}}\right) \\ $$$$\Rightarrow\mathrm{x}=−\frac{\mathrm{36}}{\mathrm{ln}\:\mathrm{10}}×\boldsymbol{\mathrm{W}}\left(\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{36}}\right) \\ $$$$\mathrm{we}\:\mathrm{will}\:\mathrm{get}\:\mathrm{here}\:\mathrm{only}\:\mathrm{one}\:\mathrm{value}\:\mathrm{for}\:\mathrm{x}. \\ $$$$ \\ $$$$\mathrm{All}\:\mathrm{solutions}\:\mathrm{are}\:\mathrm{thus} \\ $$$$\mathrm{x}=\begin{cases}{−\frac{\mathrm{36}}{\mathrm{ln}\:\mathrm{10}}×\boldsymbol{\mathrm{W}}\left(−\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{36}}\right)\:\rightarrow\:\mathrm{2}\:\mathrm{values}}\\{−\frac{\mathrm{36}}{\mathrm{ln}\:\mathrm{10}}×\boldsymbol{\mathrm{W}}\left(\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{36}}\right)\:\rightarrow\:\mathrm{1}\:\mathrm{value}}\end{cases} \\ $$

Commented by Tinkutara last updated on 12/Jun/17

In the last line how can we determine that W(((−ln 10)/(36))) has 2 values while W(((ln 10)/(36))) has one value? Can it be without Geogebra?

$$\mathrm{In}\:\mathrm{the}\:\mathrm{last}\:\mathrm{line}\:\mathrm{how}\:\mathrm{can}\:\mathrm{we}\:\mathrm{determine} \\ $$$$\mathrm{that}\:{W}\left(\frac{−\mathrm{ln}\:\mathrm{10}}{\mathrm{36}}\right)\:\mathrm{has}\:\mathrm{2}\:\mathrm{values}\:\mathrm{while} \\ $$$${W}\left(\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{36}}\right)\:\mathrm{has}\:\mathrm{one}\:\mathrm{value}?\:\mathrm{Can}\:\mathrm{it}\:\mathrm{be} \\ $$$$\mathrm{without}\:\mathrm{Geogebra}? \\ $$

Commented by mrW1 last updated on 12/Jun/17

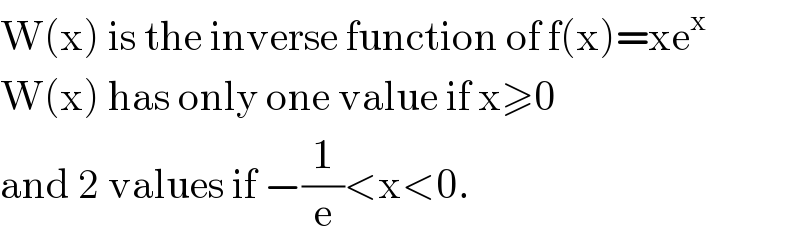
W(x) is the inverse function of f(x)=xe^x W(x) has only one value if x≥0 and 2 values if −(1/e)<x<0.

$$\mathrm{W}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{inverse}\:\mathrm{function}\:\mathrm{of}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{xe}^{\mathrm{x}} \\ $$$$\mathrm{W}\left(\mathrm{x}\right)\:\mathrm{has}\:\mathrm{only}\:\mathrm{one}\:\mathrm{value}\:\mathrm{if}\:\mathrm{x}\geqslant\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{2}\:\mathrm{values}\:\mathrm{if}\:−\frac{\mathrm{1}}{\mathrm{e}}<\mathrm{x}<\mathrm{0}. \\ $$

Commented by mrW1 last updated on 12/Jun/17

Commented by tawa tawa last updated on 12/Jun/17

2) ln(x^3 ) = (x/3) 3ln(±x) = (x/3) ln(±x) = (x/9) ((ln(±x))/(ln(10))) = (x/9) ln(±x) = ((xln(10))/9) ± x = e^((xln(10))/9) 1 = ±xe^(−((xln(10))/9)) −((xln(10))/9)e^(−((xln(10))/9)) = −((ln10)/9) −((xln(10))/9) = W[−((ln(10))/9)] x = − (9/(ln(10))) W[−((ln(10))/9)] x = − ((9(−0.3706))/(ln(10))) or x = ((9(−2.110))/(ln(10)))

$$\left.\mathrm{2}\right) \\ $$$$\mathrm{ln}\left(\mathrm{x}^{\mathrm{3}} \right)\:=\:\frac{\mathrm{x}}{\mathrm{3}} \\ $$$$\mathrm{3ln}\left(\pm\mathrm{x}\right)\:=\:\frac{\mathrm{x}}{\mathrm{3}} \\ $$$$\mathrm{ln}\left(\pm\mathrm{x}\right)\:=\:\frac{\mathrm{x}}{\mathrm{9}} \\ $$$$\frac{\mathrm{ln}\left(\pm\mathrm{x}\right)}{\mathrm{ln}\left(\mathrm{10}\right)}\:=\:\frac{\mathrm{x}}{\mathrm{9}} \\ $$$$\mathrm{ln}\left(\pm\mathrm{x}\right)\:=\:\frac{\mathrm{xln}\left(\mathrm{10}\right)}{\mathrm{9}} \\ $$$$\pm\:\mathrm{x}\:=\:\mathrm{e}^{\frac{\mathrm{xln}\left(\mathrm{10}\right)}{\mathrm{9}}} \\ $$$$\mathrm{1}\:=\:\pm\mathrm{xe}^{−\frac{\mathrm{xln}\left(\mathrm{10}\right)}{\mathrm{9}}} \\ $$$$−\frac{\mathrm{xln}\left(\mathrm{10}\right)}{\mathrm{9}}\mathrm{e}^{−\frac{\mathrm{xln}\left(\mathrm{10}\right)}{\mathrm{9}}} \:=\:−\frac{\mathrm{ln10}}{\mathrm{9}} \\ $$$$\:−\frac{\mathrm{xln}\left(\mathrm{10}\right)}{\mathrm{9}}\:=\:\mathrm{W}\left[−\frac{\mathrm{ln}\left(\mathrm{10}\right)}{\mathrm{9}}\right] \\ $$$$\:\mathrm{x}\:\:=\:−\:\frac{\mathrm{9}}{\mathrm{ln}\left(\mathrm{10}\right)}\:\mathrm{W}\left[−\frac{\mathrm{ln}\left(\mathrm{10}\right)}{\mathrm{9}}\right] \\ $$$$\mathrm{x}\:=\:\:−\:\frac{\mathrm{9}\left(−\mathrm{0}.\mathrm{3706}\right)}{\mathrm{ln}\left(\mathrm{10}\right)}\:\mathrm{or}\:\mathrm{x}\:=\:\:\frac{\mathrm{9}\left(−\mathrm{2}.\mathrm{110}\right)}{\mathrm{ln}\left(\mathrm{10}\right)}\: \\ $$

Commented by tawa tawa last updated on 12/Jun/17

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by mrW1 last updated on 12/Jun/17

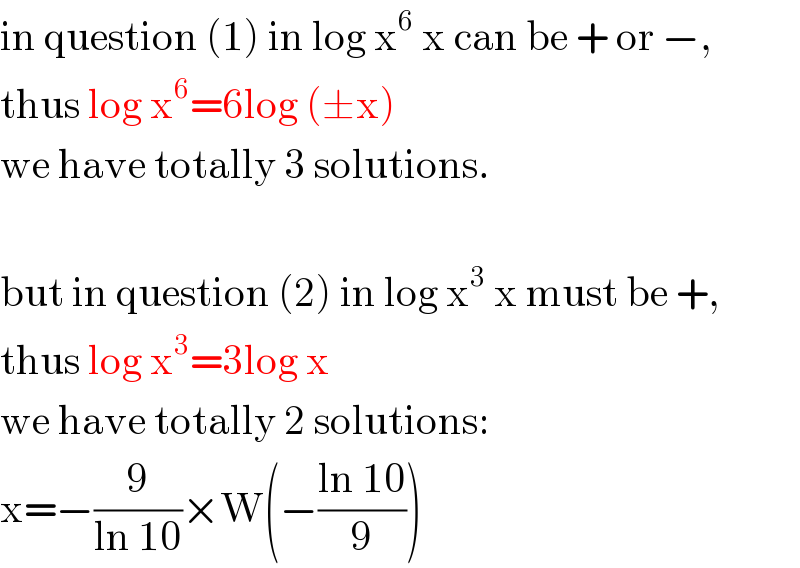
in question (1) in log x^6 x can be + or −, thus log x^6 =6log (±x) we have totally 3 solutions. but in question (2) in log x^3 x must be +, thus log x^3 =3log x we have totally 2 solutions: x=−(9/(ln 10))×W(−((ln 10)/9))

$$\mathrm{in}\:\mathrm{question}\:\left(\mathrm{1}\right)\:\mathrm{in}\:\mathrm{log}\:\mathrm{x}^{\mathrm{6}} \:\mathrm{x}\:\mathrm{can}\:\mathrm{be}\:+\:\mathrm{or}\:−, \\ $$$$\mathrm{thus}\:\mathrm{log}\:\mathrm{x}^{\mathrm{6}} =\mathrm{6log}\:\left(\pm\mathrm{x}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{totally}\:\mathrm{3}\:\mathrm{solutions}. \\ $$$$ \\ $$$$\mathrm{but}\:\mathrm{in}\:\mathrm{question}\:\left(\mathrm{2}\right)\:\mathrm{in}\:\mathrm{log}\:\mathrm{x}^{\mathrm{3}} \:\mathrm{x}\:\mathrm{must}\:\mathrm{be}\:+, \\ $$$$\mathrm{thus}\:\mathrm{log}\:\mathrm{x}^{\mathrm{3}} =\mathrm{3log}\:\mathrm{x} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{totally}\:\mathrm{2}\:\mathrm{solutions}: \\ $$$$\mathrm{x}=−\frac{\mathrm{9}}{\mathrm{ln}\:\mathrm{10}}×\mathrm{W}\left(−\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{9}}\right) \\ $$

Commented by tawa tawa last updated on 12/Jun/17

Thank you sir. i understand.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{understand}. \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 12/Jun/17

thank you so much dear mrW1. it is very beautiful and useful. god blees you master.

$${thank}\:{you}\:{so}\:{much}\:{dear}\:{mrW}\mathrm{1}. \\ $$$${it}\:{is}\:{very}\:{beautiful}\:{and}\:{useful}. \\ $$$${god}\:{blees}\:{you}\:{master}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com