Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 70898 by Henri Boucatchou last updated on 09/Oct/19

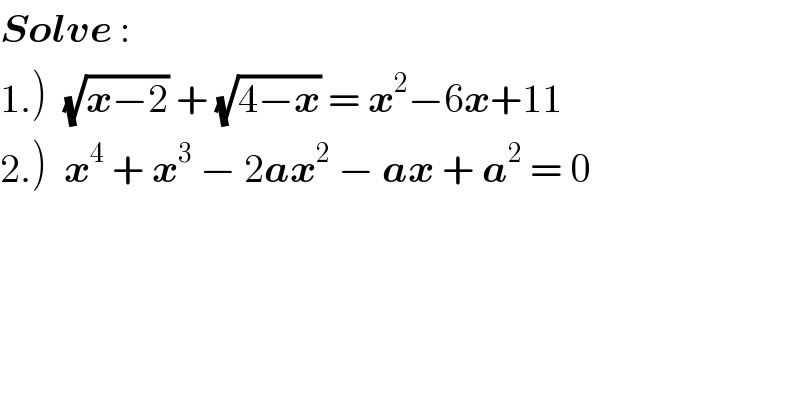
Solve : 1.) (√(x−2)) + (√(4−x)) = x^2 −6x+11 2.) x^4 + x^3 − 2ax^2 − ax + a^2 = 0

$$\boldsymbol{{Solve}}\::\: \\ $$$$\left.\mathrm{1}.\right)\:\:\sqrt{\boldsymbol{{x}}−\mathrm{2}}\:+\:\sqrt{\mathrm{4}−\boldsymbol{{x}}}\:=\:\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{6}\boldsymbol{{x}}+\mathrm{11} \\ $$$$\left.\mathrm{2}.\right)\:\:\boldsymbol{{x}}^{\mathrm{4}} \:+\:\boldsymbol{{x}}^{\mathrm{3}} \:−\:\mathrm{2}\boldsymbol{{ax}}^{\mathrm{2}} \:−\:\boldsymbol{{ax}}\:+\:\boldsymbol{{a}}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$

Answered by MJS last updated on 09/Oct/19

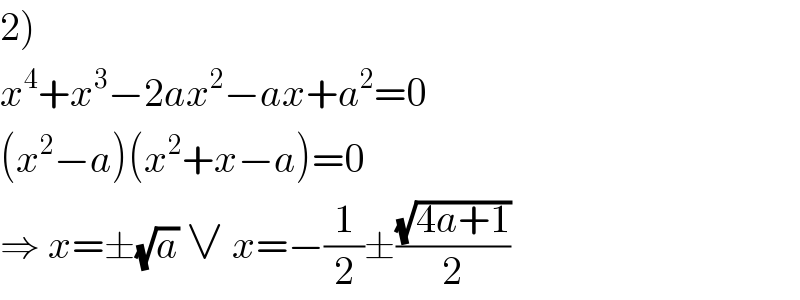
2) x^4 +x^3 −2ax^2 −ax+a^2 =0 (x^2 −a)(x^2 +x−a)=0 ⇒ x=±(√a) ∨ x=−(1/2)±((√(4a+1))/2)

$$\left.\mathrm{2}\right) \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{3}} −\mathrm{2}{ax}^{\mathrm{2}} −{ax}+{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −{a}\right)\left({x}^{\mathrm{2}} +{x}−{a}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{x}=\pm\sqrt{{a}}\:\vee\:{x}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{4}{a}+\mathrm{1}}}{\mathrm{2}} \\ $$

Answered by MJS last updated on 09/Oct/19

1) (√(x−2))+(√(4−x))=x^2 −6x+11 t=x−3 ⇔ x=t+3 (√(1−t))+(√(1+t))=t^2 +2 squaring 2+2(√(t^2 −1))=t^4 +4t^2 +4 2(√(1−t^2 ))=t^4 +4t^2 +2 squaring 4−4t^2 =8t^6 +20t^4 +16t^2 +4 t^2 (t^6 +8t^4 +20t^2 +20)=0 t_1 =t_2 =0 no other real solution ⇒ x=3

$$\left.\mathrm{1}\right) \\ $$$$\sqrt{{x}−\mathrm{2}}+\sqrt{\mathrm{4}−{x}}={x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{11} \\ $$$${t}={x}−\mathrm{3}\:\Leftrightarrow\:{x}={t}+\mathrm{3} \\ $$$$\sqrt{\mathrm{1}−{t}}+\sqrt{\mathrm{1}+{t}}={t}^{\mathrm{2}} +\mathrm{2} \\ $$$$\mathrm{squaring} \\ $$$$\mathrm{2}+\mathrm{2}\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}={t}^{\mathrm{4}} +\mathrm{4}{t}^{\mathrm{2}} +\mathrm{4} \\ $$$$\mathrm{2}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }={t}^{\mathrm{4}} +\mathrm{4}{t}^{\mathrm{2}} +\mathrm{2} \\ $$$$\mathrm{squaring} \\ $$$$\mathrm{4}−\mathrm{4}{t}^{\mathrm{2}} =\mathrm{8}{t}^{\mathrm{6}} +\mathrm{20}{t}^{\mathrm{4}} +\mathrm{16}{t}^{\mathrm{2}} +\mathrm{4} \\ $$$${t}^{\mathrm{2}} \left({t}^{\mathrm{6}} +\mathrm{8}{t}^{\mathrm{4}} +\mathrm{20}{t}^{\mathrm{2}} +\mathrm{20}\right)=\mathrm{0} \\ $$$${t}_{\mathrm{1}} ={t}_{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{no}\:\mathrm{other}\:\mathrm{real}\:\mathrm{solution} \\ $$$$\Rightarrow\:{x}=\mathrm{3} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com