
Question Number 201991 by MATHEMATICSAM last updated on 18/Dec/23
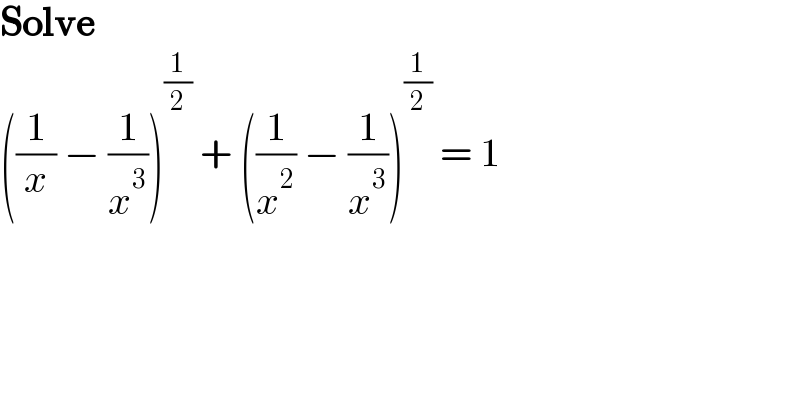
$$\boldsymbol{\mathrm{Solve}} \\ $$$$\left(\frac{\mathrm{1}}{{x}}\:−\:\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:+\:\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:=\:\mathrm{1} \\ $$
Answered by mr W last updated on 18/Dec/23
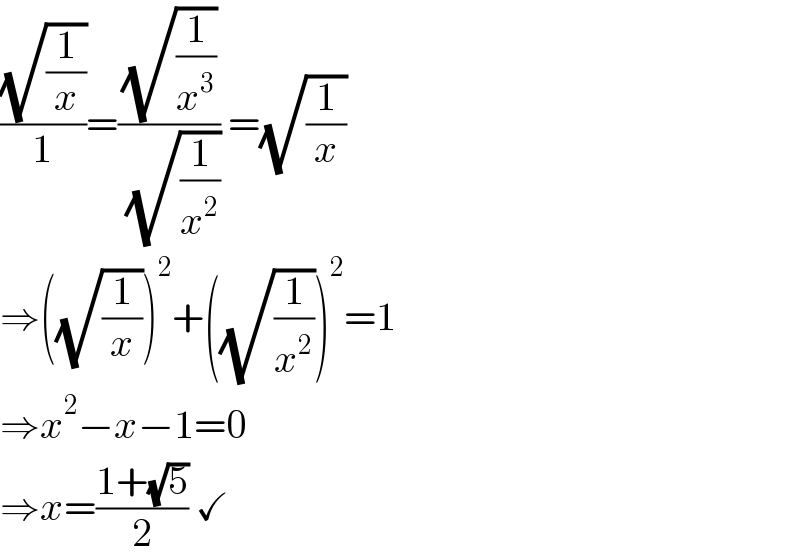
$$\frac{\sqrt{\frac{\mathrm{1}}{{x}}}}{\mathrm{1}}=\frac{\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{3}} }}}{\:\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}\:=\sqrt{\frac{\mathrm{1}}{{x}}}\: \\ $$$$\Rightarrow\left(\sqrt{\frac{\mathrm{1}}{{x}}}\right)^{\mathrm{2}} +\left(\sqrt{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −{x}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\checkmark \\ $$
Commented by mr W last updated on 19/Dec/23
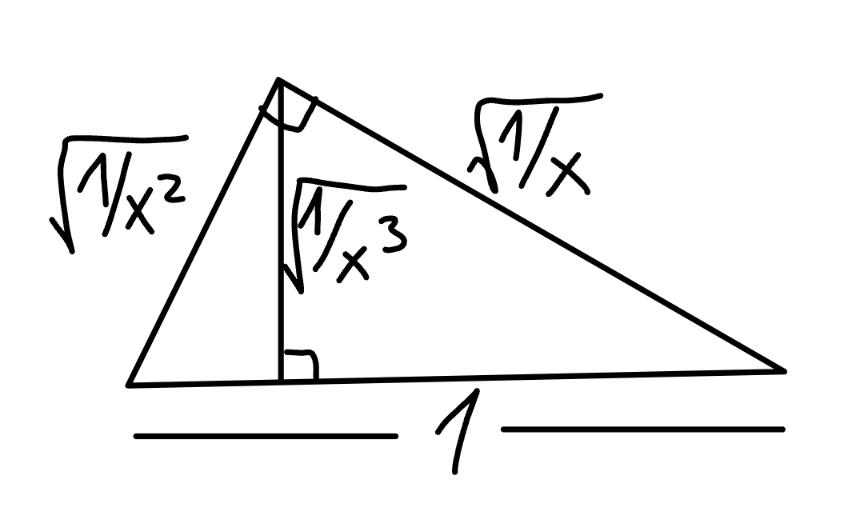
Answered by Rasheed.Sindhi last updated on 19/Dec/23
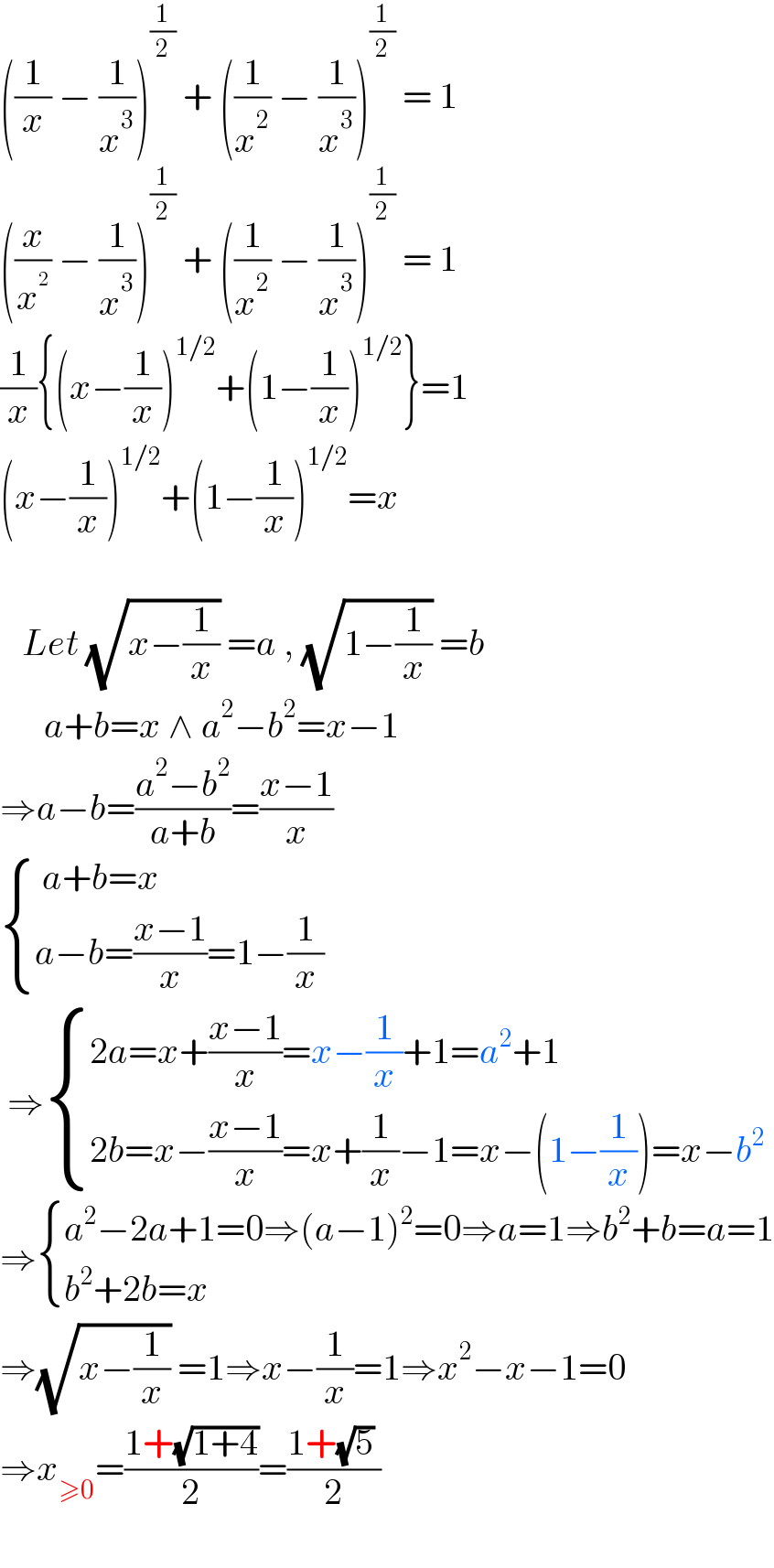
$$\left(\frac{\mathrm{1}}{{x}}\:−\:\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:+\:\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:=\:\mathrm{1} \\ $$$$\left(\frac{{x}}{{x}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:+\:\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:−\:\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:=\:\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{x}}\left\{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{1}/\mathrm{2}} +\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{1}/\mathrm{2}} \right\}=\mathrm{1} \\ $$$$\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{1}/\mathrm{2}} +\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{1}/\mathrm{2}} ={x} \\ $$$$ \\ $$$$\:\:\:{Let}\:\sqrt{{x}−\frac{\mathrm{1}}{{x}}}\:={a}\:,\:\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}}}\:={b} \\ $$$$\:\:\:\:\:\:{a}+{b}={x}\:\wedge\:{a}^{\mathrm{2}} −{b}^{\mathrm{2}} ={x}−\mathrm{1} \\ $$$$\Rightarrow{a}−{b}=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}+{b}}=\frac{{x}−\mathrm{1}}{{x}} \\ $$$$\begin{cases}{\:{a}+{b}={x}}\\{{a}−{b}=\frac{{x}−\mathrm{1}}{{x}}=\mathrm{1}−\frac{\mathrm{1}}{{x}}}\end{cases}\:\: \\ $$$$\:\Rightarrow\begin{cases}{\mathrm{2}{a}={x}+\frac{{x}−\mathrm{1}}{{x}}={x}−\frac{\mathrm{1}}{{x}}+\mathrm{1}={a}^{\mathrm{2}} +\mathrm{1}}\\{\mathrm{2}{b}={x}−\frac{{x}−\mathrm{1}}{{x}}={x}+\frac{\mathrm{1}}{{x}}−\mathrm{1}={x}−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)={x}−{b}^{\mathrm{2}} }\end{cases} \\ $$$$\Rightarrow\begin{cases}{{a}^{\mathrm{2}} −\mathrm{2}{a}+\mathrm{1}=\mathrm{0}\Rightarrow\left({a}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0}\Rightarrow{a}=\mathrm{1}\Rightarrow{b}^{\mathrm{2}} +{b}={a}=\mathrm{1}}\\{{b}^{\mathrm{2}} +\mathrm{2}{b}={x}}\end{cases} \\ $$$$\Rightarrow\sqrt{{x}−\frac{\mathrm{1}}{{x}}}\:=\mathrm{1}\Rightarrow{x}−\frac{\mathrm{1}}{{x}}=\mathrm{1}\Rightarrow{x}^{\mathrm{2}} −{x}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}_{\geqslant\mathrm{0}} =\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}}}{\mathrm{2}}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}\:}{\mathrm{2}} \\ $$$$\:\:\:\:\: \\ $$
