Question Number 134165 by liberty last updated on 28/Feb/21
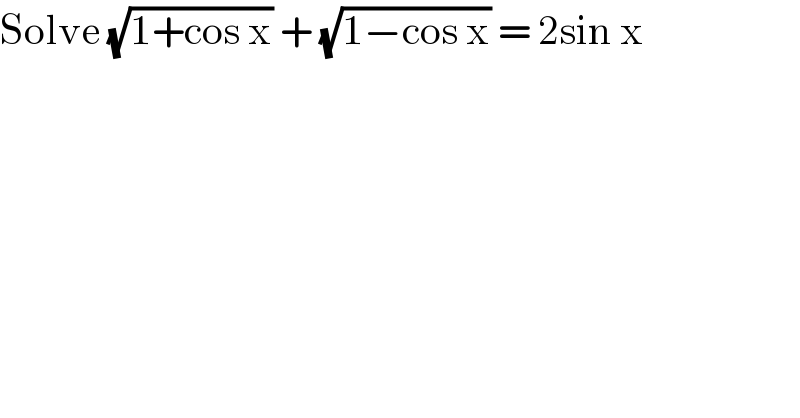
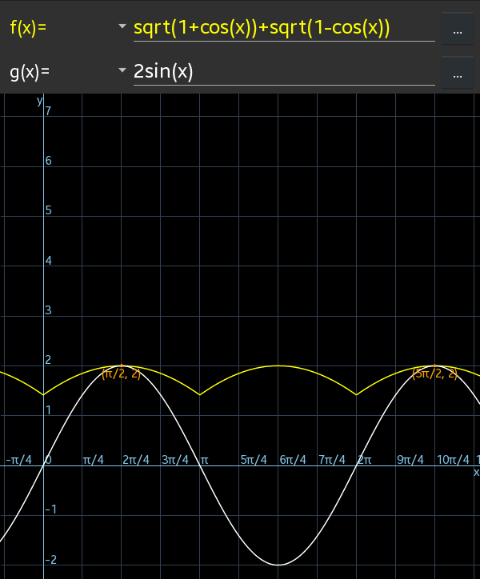
$$\mathrm{Solve}\:\sqrt{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}\:+\:\sqrt{\mathrm{1}−\mathrm{cos}\:\mathrm{x}}\:=\:\mathrm{2sin}\:\mathrm{x} \\ $$
Answered by EDWIN88 last updated on 28/Feb/21

$$\mathrm{square}\:\mathrm{both}\:\mathrm{sides} \\ $$$$\Leftrightarrow\:\mathrm{2}+\mathrm{2}\sqrt{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}\:=\:\mathrm{4sin}\:^{\mathrm{2}} \mathrm{x} \\ $$$$\Rightarrow\:\mathrm{2}+\mathrm{2}\mid\mathrm{sin}\:\mathrm{x}\mid\:=\:\mathrm{4sin}\:^{\mathrm{2}} \mathrm{x}\: \\ $$$$\Rightarrow\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}\:\pm\:\mathrm{sin}\:\mathrm{x}\:−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{x}\:=\:\frac{\pm\mathrm{1}\:\pm\mathrm{3}}{\mathrm{4}}\:\in\:\left\{−\mathrm{1},−\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}},\mathrm{2}\:\right\} \\ $$$$\mathrm{since}\:\mathrm{the}\:\mathrm{LHS}\:\mathrm{is}\:\mathrm{always}\:\mathrm{nonnegative} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{sine}\:\mathrm{on}\:\mathrm{the}\:\mathrm{right}\:\mathrm{must}\:\mathrm{be}\:\mathrm{nonnegative} \\ $$$$\mathrm{to}.\:\mathrm{Also}\:\mathrm{sin}\:\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{turns}\:\mathrm{out}\:\mathrm{to}\:\mathrm{be}\:\mathrm{wrong} \\ $$$$\mathrm{a}\:\mathrm{solution}\:\mathrm{when}\:\mathrm{we}\:\mathrm{try}\:\mathrm{to}\:\mathrm{apply}\:\mathrm{it}. \\ $$$$\mathrm{This}\:\mathrm{leaves}\:\mathrm{sin}\:\left(\mathrm{x}\right)=\mathrm{1}\:\Rightarrow\:\mathrm{x}=\mathrm{2n}\pi\:+\frac{\pi}{\mathrm{2}}\:\mathrm{or} \\ $$$$\mathrm{x}\:=\:\mathrm{2}\pi\left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$
Commented by EDWIN88 last updated on 28/Feb/21