
Question Number 197891 by Erico last updated on 02/Oct/23
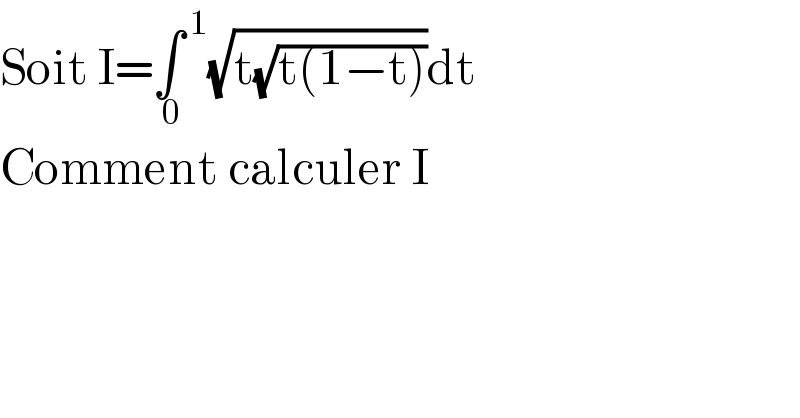
$$\mathrm{Soit}\:\mathrm{I}=\underset{\:\mathrm{0}} {\int}^{\:\mathrm{1}} \sqrt{\mathrm{t}\sqrt{\mathrm{t}\left(\mathrm{1}−\mathrm{t}\right)}}\mathrm{dt} \\ $$$$\mathrm{Comment}\:\mathrm{calculer}\:\mathrm{I} \\ $$
Answered by Mathspace last updated on 03/Oct/23
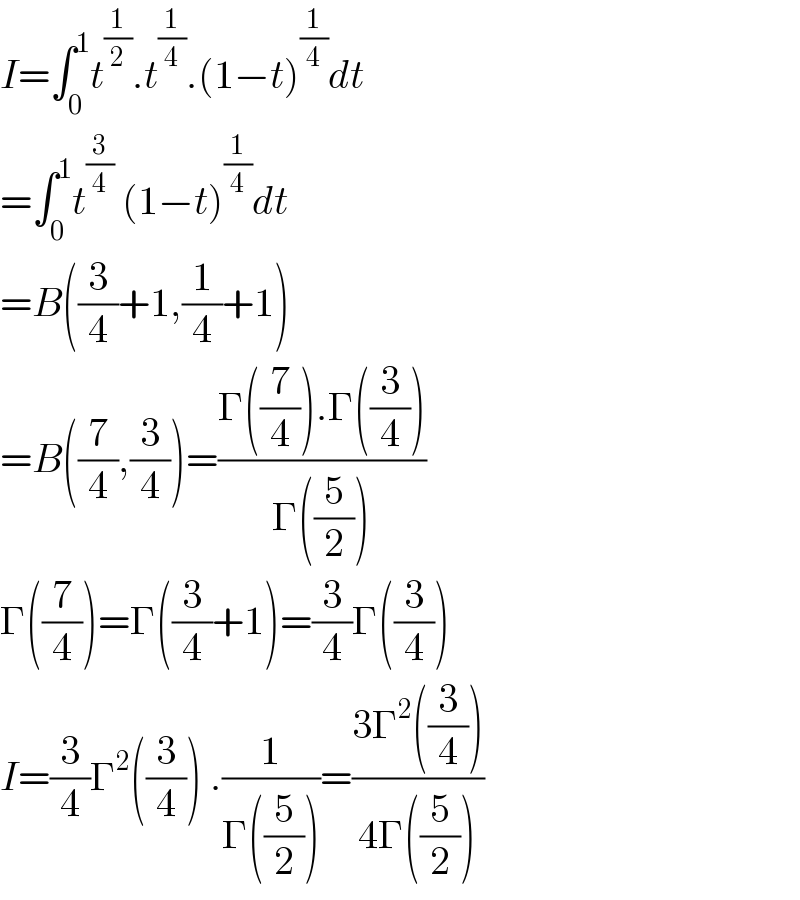
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\frac{\mathrm{1}}{\mathrm{2}}} .{t}^{\frac{\mathrm{1}}{\mathrm{4}}} .\left(\mathrm{1}−{t}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} {dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\frac{\mathrm{3}}{\mathrm{4}}} \:\left(\mathrm{1}−{t}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} {dt} \\ $$$$={B}\left(\frac{\mathrm{3}}{\mathrm{4}}+\mathrm{1},\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}\right) \\ $$$$={B}\left(\frac{\mathrm{7}}{\mathrm{4}},\frac{\mathrm{3}}{\mathrm{4}}\right)=\frac{\Gamma\left(\frac{\mathrm{7}}{\mathrm{4}}\right).\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)}{\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)} \\ $$$$\Gamma\left(\frac{\mathrm{7}}{\mathrm{4}}\right)=\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}+\mathrm{1}\right)=\frac{\mathrm{3}}{\mathrm{4}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$${I}=\frac{\mathrm{3}}{\mathrm{4}}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)\:.\frac{\mathrm{1}}{\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)}=\frac{\mathrm{3}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)}{\mathrm{4}\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)} \\ $$
Answered by Frix last updated on 02/Oct/23
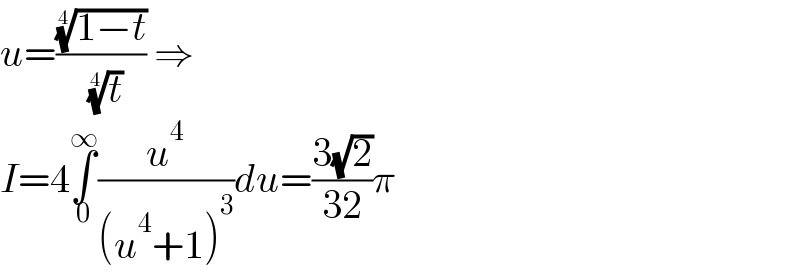
$${u}=\frac{\sqrt[{\mathrm{4}}]{\mathrm{1}−{t}}}{\:\sqrt[{\mathrm{4}}]{{t}}}\:\Rightarrow \\ $$$${I}=\mathrm{4}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{u}^{\mathrm{4}} }{\left({u}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{3}} }{du}=\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{32}}\pi \\ $$
