
Question Number 4222 by Rasheed Soomro last updated on 02/Jan/16

$${Six}\:{free}-{hand}\:{lines}\:{are}\:{drawn}\:{inside} \\ $$$${a}\:{circle}\:{in}\:{order}\:{to}\:{divide}\:{it}\:{into}\:{maximum} \\ $$$${number}\:{of}\:{parts}.{Determine}\:{this}\:{number}. \\ $$$${Note}\:{that}\:{a}\:{free}-{hand}\:{line}\:{has}\:{following} \\ $$$$\:{three}\:\:{properties}: \\ $$$$\left.{i}\right)\:{It}\:{doesn}'{t}\:{cut}\:\:{itself}. \\ $$$$\left.{ii}\right){It}\:{joins}\:{two}\:{points}\:{of}\:{circle}. \\ $$$$\left.{iii}\right)\:{It}\:{can}\:{cut}\:{another}\:{line}\:{at}\:{most}\:{at}\:{three} \\ $$$$\:\:\:\:{points}. \\ $$$${Whatif}\:{the}\:{number}\:{of}\:{lines}\:{is}\:{n}? \\ $$
Commented by prakash jain last updated on 03/Jan/16
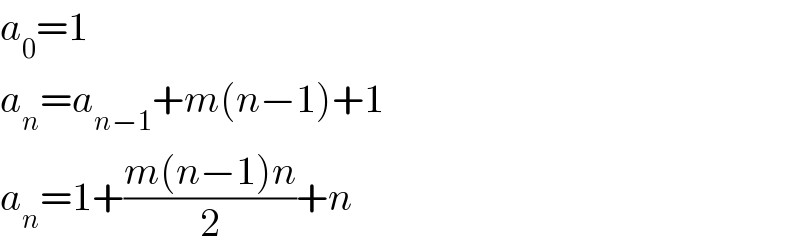
$${a}_{\mathrm{0}} =\mathrm{1} \\ $$$${a}_{{n}} ={a}_{{n}−\mathrm{1}} +{m}\left({n}−\mathrm{1}\right)+\mathrm{1} \\ $$$${a}_{{n}} =\mathrm{1}+\frac{{m}\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}+{n} \\ $$
Commented by prakash jain last updated on 03/Jan/16
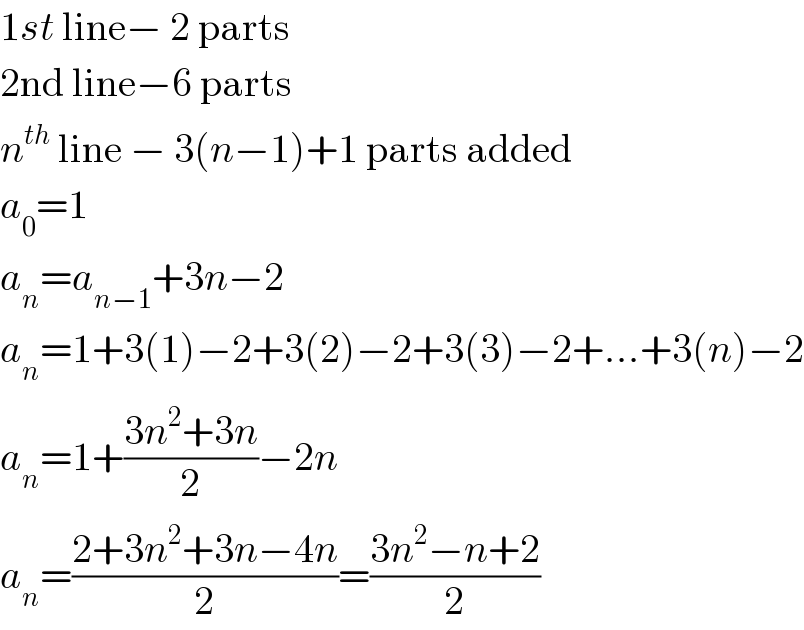
$$\mathrm{1}{st}\:\mathrm{line}−\:\mathrm{2}\:\mathrm{parts} \\ $$$$\mathrm{2nd}\:\mathrm{line}−\mathrm{6}\:\mathrm{parts} \\ $$$${n}^{{th}} \:\mathrm{line}\:−\:\mathrm{3}\left({n}−\mathrm{1}\right)+\mathrm{1}\:\mathrm{parts}\:\mathrm{added} \\ $$$${a}_{\mathrm{0}} =\mathrm{1} \\ $$$${a}_{{n}} ={a}_{{n}−\mathrm{1}} +\mathrm{3}{n}−\mathrm{2} \\ $$$${a}_{{n}} =\mathrm{1}+\mathrm{3}\left(\mathrm{1}\right)−\mathrm{2}+\mathrm{3}\left(\mathrm{2}\right)−\mathrm{2}+\mathrm{3}\left(\mathrm{3}\right)−\mathrm{2}+...+\mathrm{3}\left({n}\right)−\mathrm{2} \\ $$$${a}_{{n}} =\mathrm{1}+\frac{\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}}{\mathrm{2}}−\mathrm{2}{n} \\ $$$${a}_{{n}} =\frac{\mathrm{2}+\mathrm{3}{n}^{\mathrm{2}} +\mathrm{3}{n}−\mathrm{4}{n}}{\mathrm{2}}=\frac{\mathrm{3}{n}^{\mathrm{2}} −{n}+\mathrm{2}}{\mathrm{2}} \\ $$
Commented by Rasheed Soomro last updated on 03/Jan/16
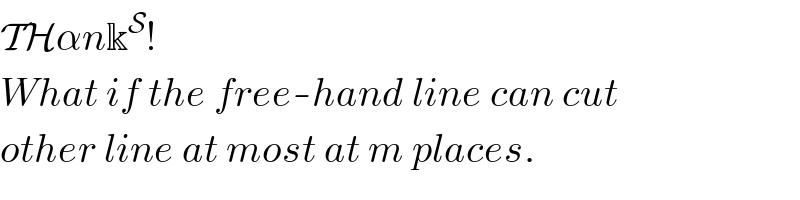
$$\mathcal{TH}\alpha{n}\Bbbk^{\mathcal{S}} ! \\ $$$${What}\:{if}\:{the}\:{free}-{hand}\:{line}\:{can}\:{cut} \\ $$$${other}\:{line}\:{at}\:{most}\:{at}\:{m}\:{places}. \\ $$
Commented by Rasheed Soomro last updated on 03/Jan/16

$$\mathbb{T}\boldsymbol{\mathrm{h}\alpha\mathrm{n}}\mathbb{X}\:\mathrm{again}! \\ $$
