Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 132302 by Lordose last updated on 13/Feb/21

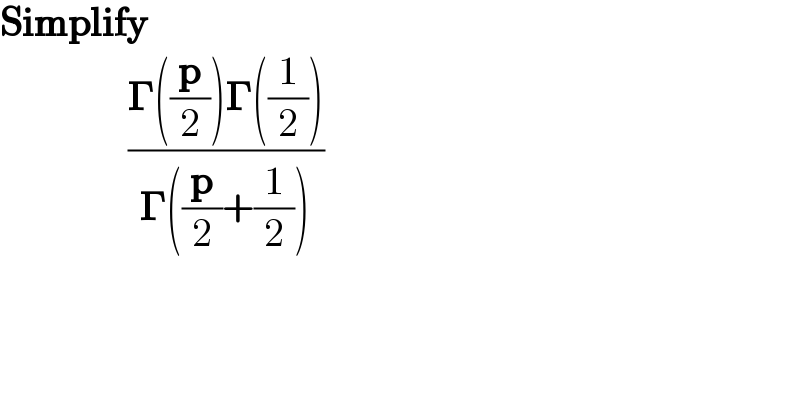
Simplify ((𝚪((p/2))𝚪((1/2)))/(𝚪((p/2)+(1/2))))

$$\boldsymbol{\mathrm{Simplify}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\boldsymbol{\Gamma}\left(\frac{\boldsymbol{\mathrm{p}}}{\mathrm{2}}\right)\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\boldsymbol{\Gamma}\left(\frac{\boldsymbol{\mathrm{p}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$

Answered by Ar Brandon last updated on 13/Feb/21

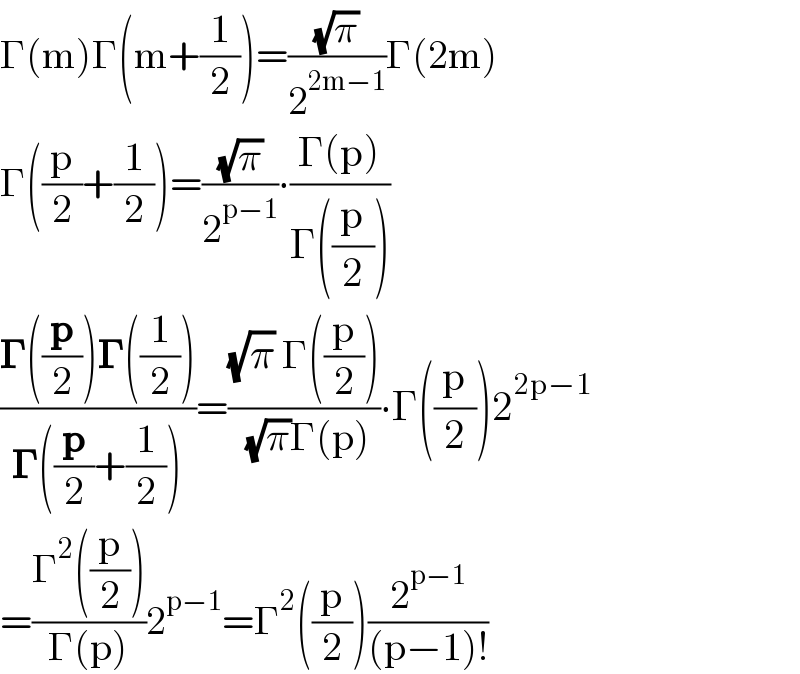
Γ(m)Γ(m+(1/2))=((√π)/2^(2m−1) )Γ(2m) Γ((p/2)+(1/2))=((√π)/2^(p−1) )∙((Γ(p))/(Γ((p/2)))) ((𝚪((p/2))𝚪((1/2)))/(𝚪((p/2)+(1/2))))=(((√π) Γ((p/2)))/( (√π)Γ(p)))∙Γ((p/2))2^(2p−1) =((Γ^2 ((p/2)))/(Γ(p)))2^(p−1) =Γ^2 ((p/2))(2^(p−1) /((p−1)!))

$$\Gamma\left(\mathrm{m}\right)\Gamma\left(\mathrm{m}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\sqrt{\pi}}{\mathrm{2}^{\mathrm{2m}−\mathrm{1}} }\Gamma\left(\mathrm{2m}\right) \\ $$$$\Gamma\left(\frac{\mathrm{p}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\sqrt{\pi}}{\mathrm{2}^{\mathrm{p}−\mathrm{1}} }\centerdot\frac{\Gamma\left(\mathrm{p}\right)}{\Gamma\left(\frac{\mathrm{p}}{\mathrm{2}}\right)} \\ $$$$\frac{\boldsymbol{\Gamma}\left(\frac{\boldsymbol{\mathrm{p}}}{\mathrm{2}}\right)\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\boldsymbol{\Gamma}\left(\frac{\boldsymbol{\mathrm{p}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}=\frac{\sqrt{\pi}\:\Gamma\left(\frac{\mathrm{p}}{\mathrm{2}}\right)}{\:\sqrt{\pi}\Gamma\left(\mathrm{p}\right)}\centerdot\Gamma\left(\frac{\mathrm{p}}{\mathrm{2}}\right)\mathrm{2}^{\mathrm{2p}−\mathrm{1}} \\ $$$$=\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{p}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{p}\right)}\mathrm{2}^{\mathrm{p}−\mathrm{1}} =\Gamma^{\mathrm{2}} \left(\frac{\mathrm{p}}{\mathrm{2}}\right)\frac{\mathrm{2}^{\mathrm{p}−\mathrm{1}} }{\left(\mathrm{p}−\mathrm{1}\right)!} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com