Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 187877 by nadovic last updated on 23/Feb/23

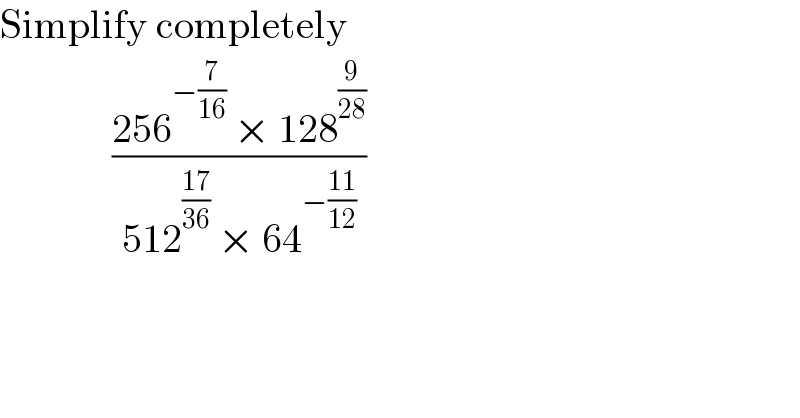
Simplify completely ((256^(−(7/(16))) × 128^(9/(28)) )/(512^((17)/(36)) × 64^(−((11)/(12))) ))

$$\mathrm{Simplify}\:\mathrm{completely} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{256}^{−\frac{\mathrm{7}}{\mathrm{16}}} \:×\:\mathrm{128}^{\frac{\mathrm{9}}{\mathrm{28}}} }{\mathrm{512}^{\frac{\mathrm{17}}{\mathrm{36}}} \:×\:\mathrm{64}^{−\frac{\mathrm{11}}{\mathrm{12}}} } \\ $$

Answered by Rasheed.Sindhi last updated on 23/Feb/23

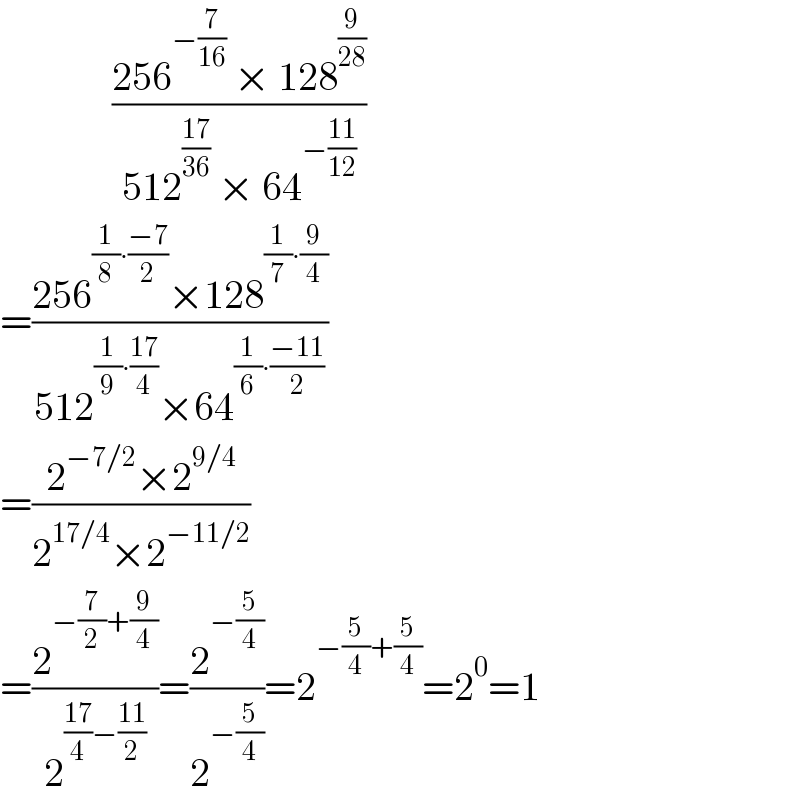
((256^(−(7/(16))) × 128^(9/(28)) )/(512^((17)/(36)) × 64^(−((11)/(12))) )) =((256^((1/8)∙((−7)/2)) ×128^((1/7)∙(9/4)) )/(512^((1/9)∙((17)/4)) ×64^((1/6)∙((−11)/2)) )) =((2^(−7/2) ×2^(9/4) )/(2^(17/4) ×2^(−11/2) )) =(2^(−(7/2)+(9/4)) /2^(((17)/4)−((11)/2)) )=(2^(−(5/4)) /2^(−(5/4)) )=2^(−(5/4)+(5/4)) =2^0 =1

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{256}^{−\frac{\mathrm{7}}{\mathrm{16}}} \:×\:\mathrm{128}^{\frac{\mathrm{9}}{\mathrm{28}}} }{\mathrm{512}^{\frac{\mathrm{17}}{\mathrm{36}}} \:×\:\mathrm{64}^{−\frac{\mathrm{11}}{\mathrm{12}}} } \\ $$$$=\frac{\mathrm{256}^{\frac{\mathrm{1}}{\mathrm{8}}\centerdot\frac{−\mathrm{7}}{\mathrm{2}}} ×\mathrm{128}^{\frac{\mathrm{1}}{\mathrm{7}}\centerdot\frac{\mathrm{9}}{\mathrm{4}}} }{\mathrm{512}^{\frac{\mathrm{1}}{\mathrm{9}}\centerdot\frac{\mathrm{17}}{\mathrm{4}}} ×\mathrm{64}^{\frac{\mathrm{1}}{\mathrm{6}}\centerdot\frac{−\mathrm{11}}{\mathrm{2}}} }\:\: \\ $$$$=\frac{\mathrm{2}^{−\mathrm{7}/\mathrm{2}} ×\mathrm{2}^{\mathrm{9}/\mathrm{4}} }{\mathrm{2}^{\mathrm{17}/\mathrm{4}} ×\mathrm{2}^{−\mathrm{11}/\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}^{−\frac{\mathrm{7}}{\mathrm{2}}+\frac{\mathrm{9}}{\mathrm{4}}} }{\mathrm{2}^{\frac{\mathrm{17}}{\mathrm{4}}−\frac{\mathrm{11}}{\mathrm{2}}} }=\frac{\mathrm{2}^{−\frac{\mathrm{5}}{\mathrm{4}}} }{\mathrm{2}^{−\frac{\mathrm{5}}{\mathrm{4}}} }=\mathrm{2}^{−\frac{\mathrm{5}}{\mathrm{4}}+\frac{\mathrm{5}}{\mathrm{4}}} =\mathrm{2}^{\mathrm{0}} =\mathrm{1} \\ $$

Commented by nadovic last updated on 23/Feb/23

Wow.. Thank you Sir

$${Wow}..\:{Thank}\:{you}\:{Sir} \\ $$

Answered by HeferH last updated on 23/Feb/23

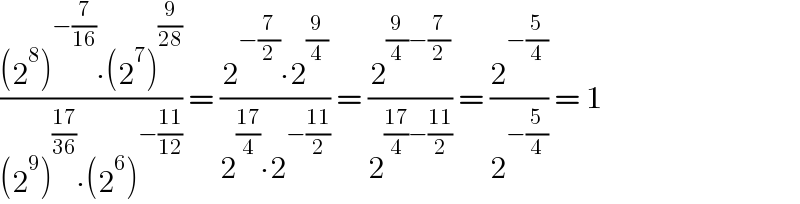
(((2^8 )^(−(7/(16))) ∙(2^7 )^(9/(28)) )/((2^9 )^((17)/(36)) ∙(2^6 )^(−((11)/(12))) )) = ((2^(−(7/2)) ∙2^(9/4) )/(2^((17)/4) ∙2^(−((11)/2)) )) = (2^((9/4)−(7/2)) /2^(((17)/4)−((11)/2)) ) = (2^(−(5/4)) /2^(−(5/4)) ) = 1

$$\frac{\left(\mathrm{2}^{\mathrm{8}} \right)^{−\frac{\mathrm{7}}{\mathrm{16}}} \centerdot\left(\mathrm{2}^{\mathrm{7}} \right)^{\frac{\mathrm{9}}{\mathrm{28}}} }{\left(\mathrm{2}^{\mathrm{9}} \right)^{\frac{\mathrm{17}}{\mathrm{36}}} \centerdot\left(\mathrm{2}^{\mathrm{6}} \right)^{−\frac{\mathrm{11}}{\mathrm{12}}} }\:=\:\frac{\mathrm{2}^{−\frac{\mathrm{7}}{\mathrm{2}}} \centerdot\mathrm{2}^{\frac{\mathrm{9}}{\mathrm{4}}} }{\mathrm{2}^{\frac{\mathrm{17}}{\mathrm{4}}} \centerdot\mathrm{2}^{−\frac{\mathrm{11}}{\mathrm{2}}} }\:=\:\frac{\mathrm{2}^{\frac{\mathrm{9}}{\mathrm{4}}−\frac{\mathrm{7}}{\mathrm{2}}} }{\mathrm{2}^{\frac{\mathrm{17}}{\mathrm{4}}−\frac{\mathrm{11}}{\mathrm{2}}} }\:=\:\frac{\mathrm{2}^{−\frac{\mathrm{5}}{\mathrm{4}}} }{\mathrm{2}^{−\frac{\mathrm{5}}{\mathrm{4}}} }\:=\:\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com