
Question Number 178434 by Spillover last updated on 16/Oct/22
![Simplify by using law of algebra (a) [p∨(p∧q)]→∼p (b)(p∧q)→q](Q178434.png)
$$\mathrm{Simplify}\:\mathrm{by}\:\mathrm{using}\:\mathrm{law}\:\mathrm{of}\:\mathrm{algebra} \\ $$$$\left(\mathrm{a}\right)\:\left[\mathrm{p}\vee\left(\mathrm{p}\wedge\mathrm{q}\right)\right]\rightarrow\sim\mathrm{p} \\ $$$$\left(\mathrm{b}\right)\left(\mathrm{p}\wedge\mathrm{q}\right)\rightarrow\mathrm{q} \\ $$
Answered by Spillover last updated on 16/Oct/22

Answered by cortano1 last updated on 16/Oct/22

$$\left(\mathrm{a}\right)\:\left[\mathrm{p}\vee\left(\mathrm{p}\wedge\mathrm{q}\right)\right)\Rightarrow\sim\mathrm{p} \\ $$$$\:\:\:\:\:\:=\:\mathrm{p}\Rightarrow\sim\mathrm{p} \\ $$$$\:\:\:\:\:=\:\sim\mathrm{p}\vee\sim\mathrm{p}\:=\:\sim\mathrm{p} \\ $$
Commented by Spillover last updated on 16/Oct/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by Spillover last updated on 16/Oct/22
$${yours}\:{is}\:{the}\:{best}\:{and}\:{easiest} \\ $$
Answered by cortano1 last updated on 16/Oct/22
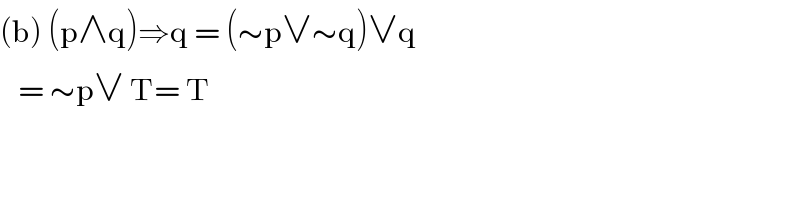
$$\left(\mathrm{b}\right)\:\left(\mathrm{p}\wedge\mathrm{q}\right)\Rightarrow\mathrm{q}\:=\:\left(\sim\mathrm{p}\vee\sim\mathrm{q}\right)\vee\mathrm{q} \\ $$$$\:\:\:=\:\sim\mathrm{p}\vee\:\mathrm{T}=\:\mathrm{T} \\ $$
Commented by Spillover last updated on 16/Oct/22

$$\mathrm{thanks} \\ $$
Commented by SLVR last updated on 16/Oct/22

$${nice}\:{sir}.. \\ $$
