Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 88899 by Ar Brandon last updated on 13/Apr/20

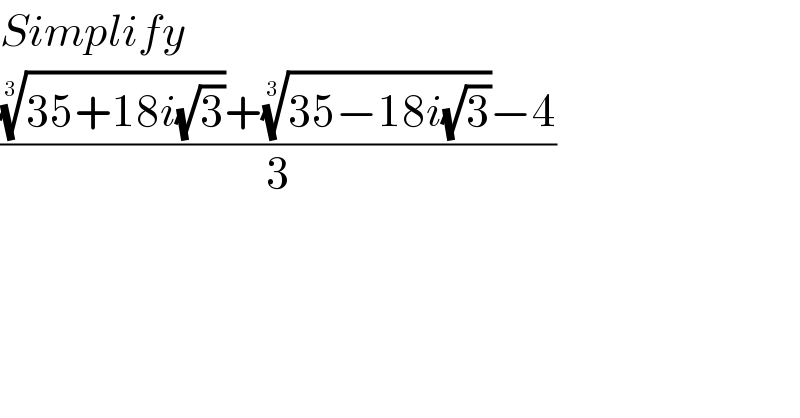
Simplify ((((35+18i(√3)))^(1/3) +((35−18i(√3)))^(1/3) −4)/3)

$${Simplify} \\ $$$$\frac{\sqrt[{\mathrm{3}}]{\mathrm{35}+\mathrm{18}{i}\sqrt{\mathrm{3}}}+\sqrt[{\mathrm{3}}]{\mathrm{35}−\mathrm{18}{i}\sqrt{\mathrm{3}}}−\mathrm{4}}{\mathrm{3}} \\ $$

Commented by naka3546 last updated on 14/Apr/20

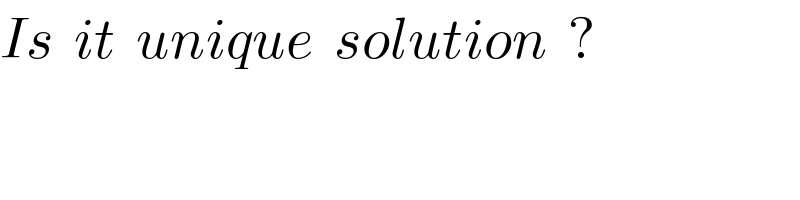
Is it unique solution ?

$${Is}\:\:{it}\:\:{unique}\:\:{solution}\:\:? \\ $$

Commented by MJS last updated on 14/Apr/20

usually you get something like this when solving a polynome of 3^(rd) degree using Cardano although D=(p^3 /(27))+(q^2 /4)<0. In these cases Cardano doesn′t work −(q/2)±(√((p^3 /(27))+(q^2 /4)))=35±(√(−972)) ⇒ p=−39∧q=−70 x^3 −39x−70=0 trying factors of 70 ⇒ ⇒ x_1 =−5∧x_2 =−2∧x_3 =7 knowing that the angle of 35+18(√3)i is within [0; (π/2)] the sum of the roots must be >0 ⇒ ((35+18(√3)i))^(1/3) +((35−18(√3)i))^(1/3) =7 ⇒ answer is 1

$$\mathrm{usually}\:\mathrm{you}\:\mathrm{get}\:\mathrm{something}\:\mathrm{like}\:\mathrm{this}\:\mathrm{when} \\ $$$$\mathrm{solving}\:\mathrm{a}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{degree}\:\mathrm{using} \\ $$$$\mathrm{Cardano}\:\mathrm{although}\:{D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}<\mathrm{0}.\:\mathrm{In}\:\mathrm{these} \\ $$$$\mathrm{cases}\:\mathrm{Cardano}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{work} \\ $$$$−\frac{{q}}{\mathrm{2}}\pm\sqrt{\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}}=\mathrm{35}\pm\sqrt{−\mathrm{972}} \\ $$$$\Rightarrow\:{p}=−\mathrm{39}\wedge{q}=−\mathrm{70} \\ $$$${x}^{\mathrm{3}} −\mathrm{39}{x}−\mathrm{70}=\mathrm{0} \\ $$$$\mathrm{trying}\:\mathrm{factors}\:\mathrm{of}\:\mathrm{70}\:\Rightarrow \\ $$$$\Rightarrow\:{x}_{\mathrm{1}} =−\mathrm{5}\wedge{x}_{\mathrm{2}} =−\mathrm{2}\wedge{x}_{\mathrm{3}} =\mathrm{7} \\ $$$$\mathrm{knowing}\:\mathrm{that}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{35}+\mathrm{18}\sqrt{\mathrm{3}}\mathrm{i}\:\mathrm{is}\:\mathrm{within} \\ $$$$\left[\mathrm{0};\:\frac{\pi}{\mathrm{2}}\right]\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{must}\:\mathrm{be}\:>\mathrm{0} \\ $$$$\Rightarrow\:\sqrt[{\mathrm{3}}]{\mathrm{35}+\mathrm{18}\sqrt{\mathrm{3}}\mathrm{i}}+\sqrt[{\mathrm{3}}]{\mathrm{35}−\mathrm{18}\sqrt{\mathrm{3}}\mathrm{i}}=\mathrm{7} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{1} \\ $$

Commented by Ar Brandon last updated on 14/Apr/20

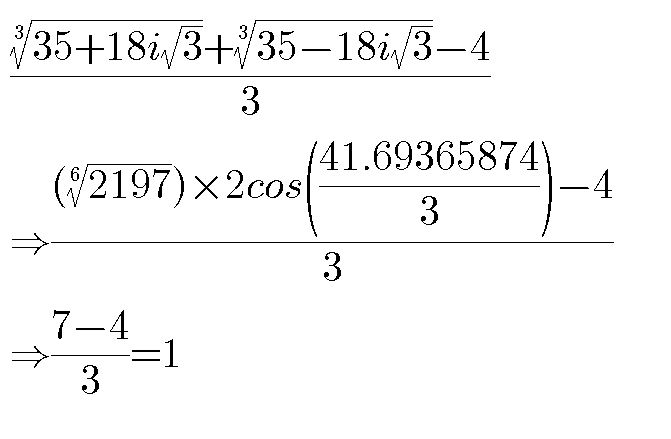
Commented by Ar Brandon last updated on 14/Apr/20

I think it goes in all cases. Just need to manipulate the complex numbers.

$${I}\:{think}\:{it}\:{goes}\:{in}\:{all}\:{cases}.\:{Just}\:{need}\:{to} \\ $$$${manipulate}\:{the}\:{complex}\:{numbers}. \\ $$

Commented by MJS last updated on 14/Apr/20

but it is not recommended x^3 +ax^2 +bx+c=0 first, try factors of c second, let x=z−(a/3) ⇒ x^3 +px+q=0 D=(p^3 /(27))+(q^2 /4) ⇒ { ((Cardano; D>0)),((trigonometric solution; D<0)) :} try this one using Cardano, exact solutions required: x^3 −8x^2 −154x+332=0

$$\mathrm{but}\:\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{recommended} \\ $$$${x}^{\mathrm{3}} +{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$$\mathrm{first},\:\mathrm{try}\:\mathrm{factors}\:\mathrm{of}\:{c} \\ $$$$\mathrm{second},\:\mathrm{let}\:{x}={z}−\frac{{a}}{\mathrm{3}} \\ $$$$\Rightarrow\:{x}^{\mathrm{3}} +{px}+{q}=\mathrm{0} \\ $$$${D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow\:\begin{cases}{\mathrm{Cardano};\:{D}>\mathrm{0}}\\{\mathrm{trigonometric}\:\mathrm{solution};\:{D}<\mathrm{0}}\end{cases} \\ $$$$\mathrm{try}\:\mathrm{this}\:\mathrm{one}\:\mathrm{using}\:\mathrm{Cardano},\:\mathrm{exact}\:\mathrm{solutions} \\ $$$$\mathrm{required}: \\ $$$${x}^{\mathrm{3}} −\mathrm{8}{x}^{\mathrm{2}} −\mathrm{154}{x}+\mathrm{332}=\mathrm{0} \\ $$

Commented by Ar Brandon last updated on 02/May/20

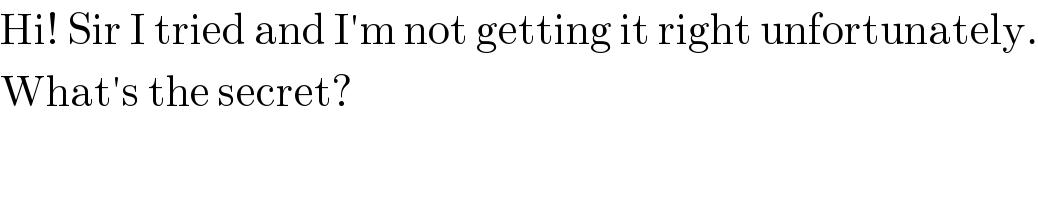
Hi! Sir I tried and I′m not getting it right unfortunately. What′s the secret?

$$\mathrm{Hi}!\:\mathrm{Sir}\:\mathrm{I}\:\mathrm{tried}\:\mathrm{and}\:\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{getting}\:\mathrm{it}\:\mathrm{right}\:\mathrm{unfortunately}. \\ $$$$\mathrm{What}'\mathrm{s}\:\mathrm{the}\:\mathrm{secret}? \\ $$

Commented by Ar Brandon last updated on 02/May/20

What PDF document would you recommend me to study in other to master the subject ? ����

Commented by MJS last updated on 02/May/20

I will after the weekend... if I forget, please remind me

$$\mathrm{I}\:\mathrm{will}\:\mathrm{after}\:\mathrm{the}\:\mathrm{weekend}...\:\mathrm{if}\:\mathrm{I}\:\mathrm{forget},\:\mathrm{please} \\ $$$$\mathrm{remind}\:\mathrm{me} \\ $$

Commented by Ar Brandon last updated on 02/May/20

OK thanks

$$\mathrm{OK}\:\mathrm{thanks}\: \\ $$

Commented by Ar Brandon last updated on 05/May/20

Hi Sir ; just to remind you as you said. ��

Commented by MJS last updated on 05/May/20

I only found one pdf in German but there′s an article on Wikipedia, search for “Wikipedia cubic equation”

$$\mathrm{I}\:\mathrm{only}\:\mathrm{found}\:\mathrm{one}\:\mathrm{pdf}\:\mathrm{in}\:\mathrm{German} \\ $$$$\mathrm{but}\:\mathrm{there}'\mathrm{s}\:\mathrm{an}\:\mathrm{article}\:\mathrm{on}\:\mathrm{Wikipedia},\:\mathrm{search} \\ $$$$\mathrm{for}\:``\mathrm{Wikipedia}\:\mathrm{cubic}\:\mathrm{equation}'' \\ $$

Commented by Ar Brandon last updated on 05/May/20

OK, there's no problem. What German PDF did you find ? ��

Commented by MJS last updated on 05/May/20

http://mathemator.org/Media/Themen/Kubische%20Gleichungen.pdf

Commented by Ar Brandon last updated on 05/May/20

thank you Sir ��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com