Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 196242 by pete last updated on 20/Aug/23

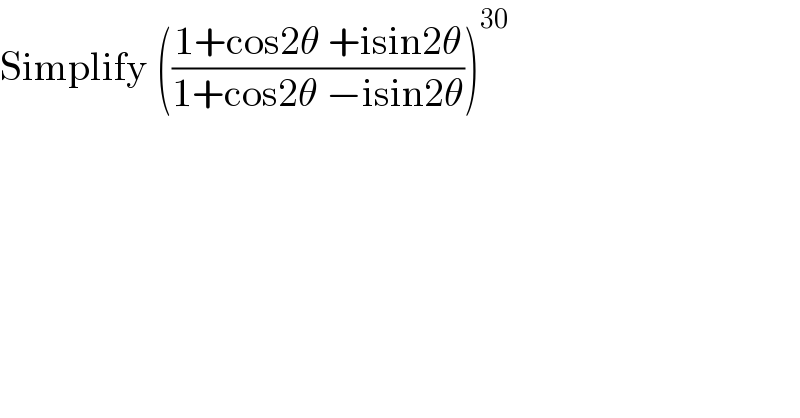
Simplify (((1+cos2θ +isin2θ)/(1+cos2θ −isin2θ)))^(30)

$$\mathrm{Simplify}\:\left(\frac{\mathrm{1}+\mathrm{cos2}\theta\:+\mathrm{isin2}\theta}{\mathrm{1}+\mathrm{cos2}\theta\:−\mathrm{isin2}\theta}\right)^{\mathrm{30}} \\ $$

Answered by MM42 last updated on 20/Aug/23

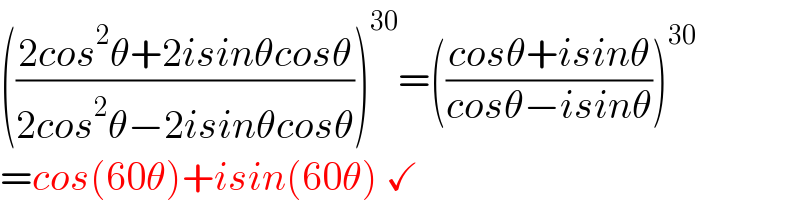
(((2cos^2 θ+2isinθcosθ)/(2cos^2 θ−2isinθcosθ)))^(30) =(((cosθ+isinθ)/(cosθ−isinθ)))^(30) =cos(60θ)+isin(60θ) ✓

$$\left(\frac{\mathrm{2}{cos}^{\mathrm{2}} \theta+\mathrm{2}{isin}\theta{cos}\theta}{\mathrm{2}{cos}^{\mathrm{2}} \theta−\mathrm{2}{isin}\theta{cos}\theta}\right)^{\mathrm{30}} =\left(\frac{{cos}\theta+{isin}\theta}{{cos}\theta−{isin}\theta}\right)^{\mathrm{30}} \\ $$$$={cos}\left(\mathrm{60}\theta\right)+{isin}\left(\mathrm{60}\theta\right)\:\checkmark \\ $$

Answered by Frix last updated on 20/Aug/23

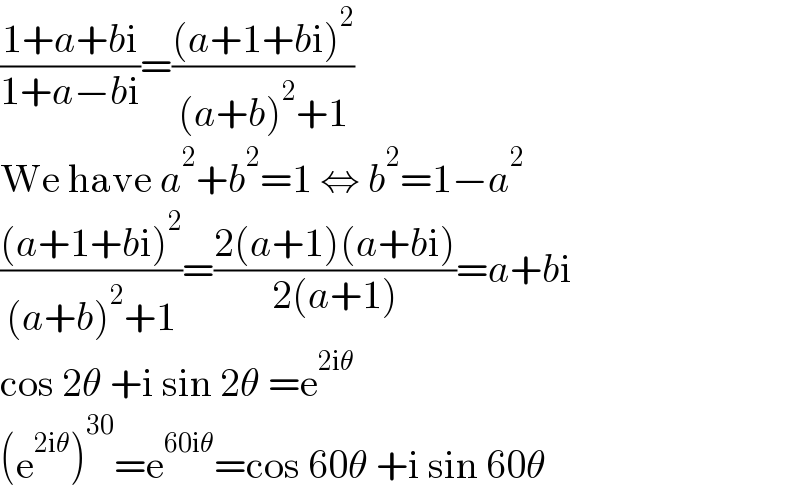
((1+a+bi)/(1+a−bi))=(((a+1+bi)^2 )/((a+b)^2 +1)) We have a^2 +b^2 =1 ⇔ b^2 =1−a^2 (((a+1+bi)^2 )/((a+b)^2 +1))=((2(a+1)(a+bi))/(2(a+1)))=a+bi cos 2θ +i sin 2θ =e^(2iθ) (e^(2iθ) )^(30) =e^(60iθ) =cos 60θ +i sin 60θ

$$\frac{\mathrm{1}+{a}+{b}\mathrm{i}}{\mathrm{1}+{a}−{b}\mathrm{i}}=\frac{\left({a}+\mathrm{1}+{b}\mathrm{i}\right)^{\mathrm{2}} }{\left({a}+{b}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{We}\:\mathrm{have}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{1}\:\Leftrightarrow\:{b}^{\mathrm{2}} =\mathrm{1}−{a}^{\mathrm{2}} \\ $$$$\frac{\left({a}+\mathrm{1}+{b}\mathrm{i}\right)^{\mathrm{2}} }{\left({a}+{b}\right)^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{2}\left({a}+\mathrm{1}\right)\left({a}+{b}\mathrm{i}\right)}{\mathrm{2}\left({a}+\mathrm{1}\right)}={a}+{b}\mathrm{i} \\ $$$$\mathrm{cos}\:\mathrm{2}\theta\:+\mathrm{i}\:\mathrm{sin}\:\mathrm{2}\theta\:=\mathrm{e}^{\mathrm{2i}\theta} \\ $$$$\left(\mathrm{e}^{\mathrm{2i}\theta} \right)^{\mathrm{30}} =\mathrm{e}^{\mathrm{60i}\theta} =\mathrm{cos}\:\mathrm{60}\theta\:+\mathrm{i}\:\mathrm{sin}\:\mathrm{60}\theta \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com