Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 197089 by pete last updated on 07/Sep/23

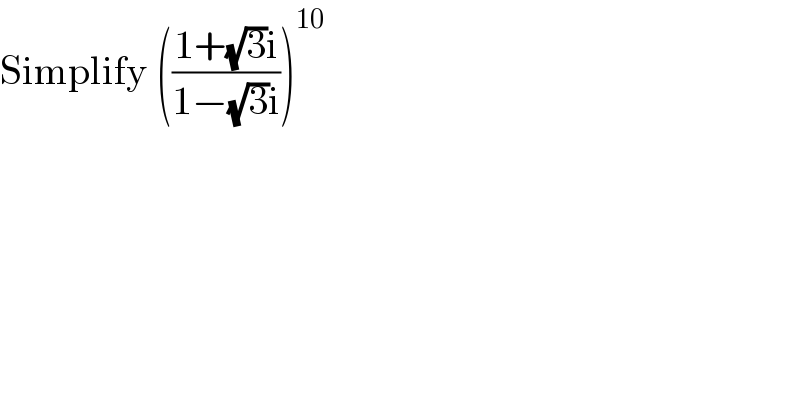
Simplify (((1+(√3)i)/(1−(√3)i)))^(10)

$$\mathrm{Simplify}\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{i}}{\mathrm{1}−\sqrt{\mathrm{3}}\mathrm{i}}\right)^{\mathrm{10}} \\ $$

Answered by JDamian last updated on 07/Sep/23

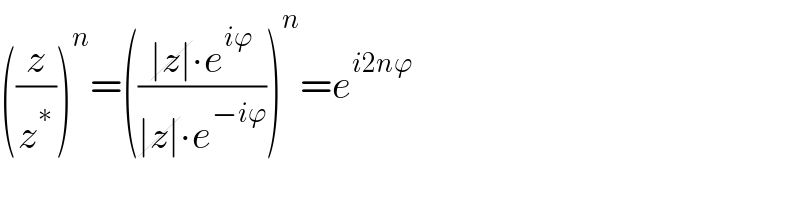
((z/z^∗ ))^n =(((∣z∣∙e^(iϕ) )/(∣z∣∙e^(−iϕ) )))^n =e^(i2nϕ)

$$\left(\frac{{z}}{{z}^{\ast} }\right)^{{n}} =\left(\frac{\cancel{\mid{z}\mid}\centerdot{e}^{{i}\varphi} }{\cancel{\mid{z}\mid}\centerdot{e}^{−{i}\varphi} }\right)^{{n}} ={e}^{{i}\mathrm{2}{n}\varphi} \\ $$

Commented by MM42 last updated on 08/Sep/23

⋛

$$\:\underline{\underbrace{\lesseqgtr}} \\ $$

Commented by pete last updated on 07/Sep/23

thank you sir,but i will be glad if you can offer some further explanation

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir},\mathrm{but}\:\mathrm{i}\:\mathrm{will}\:\mathrm{be}\:\mathrm{glad}\:\mathrm{if}\:\mathrm{you}\:\mathrm{can}\:\mathrm{offer}\: \\ $$$$\mathrm{some}\:\mathrm{further}\:\mathrm{explanation} \\ $$

Commented by MM42 last updated on 08/Sep/23

you should study more about complex number

$${you}\:{should}\:{study}\:{more}\:{about}\:{complex}\:{number} \\ $$

Commented by pete last updated on 07/Sep/23

I have heard you, sir. Sir can you recommend a book for me?

$$\mathrm{I}\:\mathrm{have}\:\mathrm{heard}\:\mathrm{you},\:\mathrm{sir}. \\ $$$$\mathrm{Sir}\:\mathrm{can}\:\mathrm{you}\:\mathrm{recommend}\:\mathrm{a}\:\mathrm{book}\:\mathrm{for}\:\mathrm{me}? \\ $$

Answered by Frix last updated on 08/Sep/23

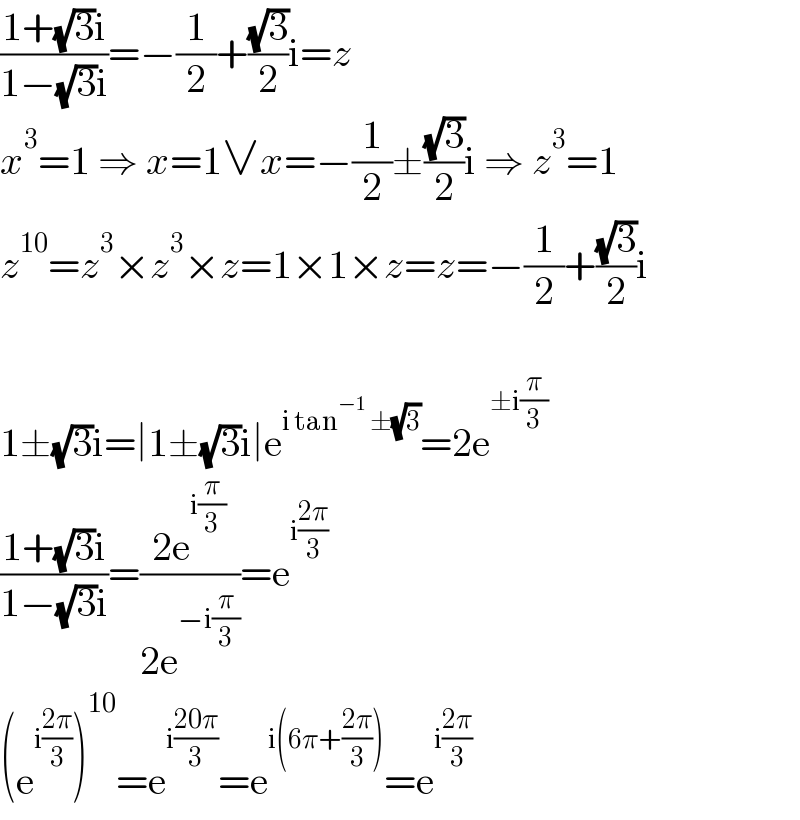
((1+(√3)i)/(1−(√3)i))=−(1/2)+((√3)/2)i=z x^3 =1 ⇒ x=1∨x=−(1/2)±((√3)/2)i ⇒ z^3 =1 z^(10) =z^3 ×z^3 ×z=1×1×z=z=−(1/2)+((√3)/2)i 1±(√3)i=∣1±(√3)i∣e^(i tan^(−1) ±(√3)) =2e^(±i(π/3)) ((1+(√3)i)/(1−(√3)i))=((2e^(i(π/3)) )/(2e^(−i(π/3)) ))=e^(i((2π)/3)) (e^(i((2π)/3)) )^(10) =e^(i((20π)/3)) =e^(i(6π+((2π)/3))) =e^(i((2π)/3))

$$\frac{\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{i}}{\mathrm{1}−\sqrt{\mathrm{3}}\mathrm{i}}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}={z} \\ $$$${x}^{\mathrm{3}} =\mathrm{1}\:\Rightarrow\:{x}=\mathrm{1}\vee{x}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\:\Rightarrow\:{z}^{\mathrm{3}} =\mathrm{1} \\ $$$${z}^{\mathrm{10}} ={z}^{\mathrm{3}} ×{z}^{\mathrm{3}} ×{z}=\mathrm{1}×\mathrm{1}×{z}={z}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$$$ \\ $$$$\mathrm{1}\pm\sqrt{\mathrm{3}}\mathrm{i}=\mid\mathrm{1}\pm\sqrt{\mathrm{3}}\mathrm{i}\mid\mathrm{e}^{\mathrm{i}\:\mathrm{tan}^{−\mathrm{1}} \:\pm\sqrt{\mathrm{3}}} =\mathrm{2e}^{\pm\mathrm{i}\frac{\pi}{\mathrm{3}}} \\ $$$$\frac{\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{i}}{\mathrm{1}−\sqrt{\mathrm{3}}\mathrm{i}}=\frac{\mathrm{2e}^{\mathrm{i}\frac{\pi}{\mathrm{3}}} }{\mathrm{2e}^{−\mathrm{i}\frac{\pi}{\mathrm{3}}} }=\mathrm{e}^{\mathrm{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \\ $$$$\left(\mathrm{e}^{\mathrm{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \right)^{\mathrm{10}} =\mathrm{e}^{\mathrm{i}\frac{\mathrm{20}\pi}{\mathrm{3}}} =\mathrm{e}^{\mathrm{i}\left(\mathrm{6}\pi+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)} =\mathrm{e}^{\mathrm{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com