Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 188151 by Shrinava last updated on 26/Feb/23

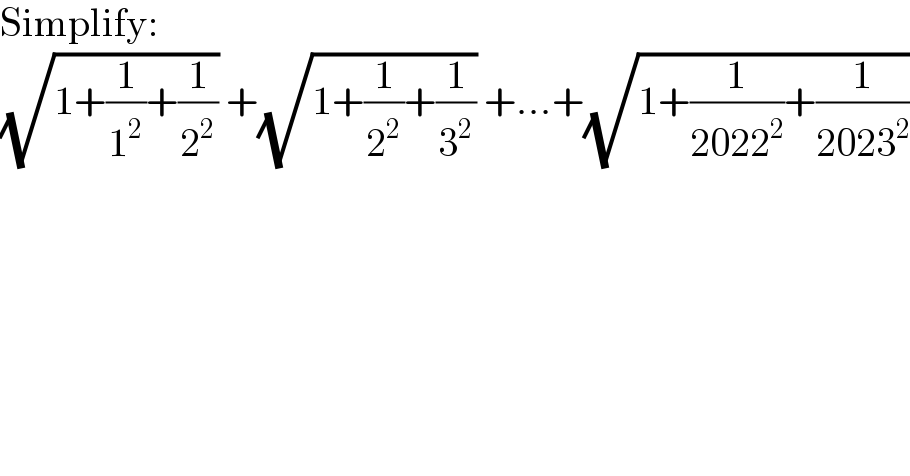
Simplify: (√(1+(1/1^2 )+(1/2^2 ))) +(√(1+(1/2^2 )+(1/3^2 ))) +...+(√(1+(1/(2022^2 ))+(1/(2023^2 ))))

$$\mathrm{Simplify}: \\ $$$$\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }}\:+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }}\:+...+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2022}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2023}^{\mathrm{2}} }} \\ $$

Answered by BaliramKumar last updated on 27/Feb/23

Solution:− (√(1+(1/1^2 )+(1/2^2 ))) +(√(1+(1/2^2 )+(1/3^2 ))) +...+(√(1+(1/(2022^2 ))+(1/(2023^2 )))) t_1 =(√(1+(1/1^2 )+(1/2^2 ) )) = (√(1+1+(1/4) )) = (√((9/4) )) = (3/2) t_2 =(√(1+ (1/2^2 )+(1/3^2 ))) = (√(1+(1/4)+(1/9))) = (√(((49)/(36)) )) = (7/6) t_3 =(√(1+ (1/3^2 )+(1/4^2 ))) = (√(1+(1/9)+(1/(16)))) = (√(((169)/(144)) )) = ((13)/(12)) t_4 .............. t_(5..............) t_(2022) = (√(1+(1/(2022^2 ))+(1/(2023^2 )))) S_1 = t_1 = (3/2)=1+(1/2)=1(1/2) S_2 = S_1 +t_2 = (3/2)+(7/6)= ((16)/6) =(8/3)=2+(2/3)=2(2/3) S_3 = S_2 +t_3 = (8/3)+((13)/(12))= ((45)/(12))=((15)/4)=3+(3/4) = 3(3/4) S_(4..........) S_(2022) = 2022+((2022)/(2023)) = determinant (((2022((2022)/(2023)))))Answer

$${Solution}:− \\ $$$$\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }}\:+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }}\:+...+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2022}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2023}^{\mathrm{2}} }} \\ $$$${t}_{\mathrm{1}} =\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:}\:=\:\sqrt{\mathrm{1}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\:}\:=\:\sqrt{\frac{\mathrm{9}}{\mathrm{4}}\:}\:=\:\frac{\mathrm{3}}{\mathrm{2}}\: \\ $$$${t}_{\mathrm{2}} \:=\sqrt{\mathrm{1}+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }}\:=\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{9}}}\:=\:\sqrt{\frac{\mathrm{49}}{\mathrm{36}}\:}\:=\:\frac{\mathrm{7}}{\mathrm{6}}\:\: \\ $$$${t}_{\mathrm{3}} \:=\sqrt{\mathrm{1}+\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }}\:=\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{16}}}\:=\:\sqrt{\frac{\mathrm{169}}{\mathrm{144}}\:}\:=\:\frac{\mathrm{13}}{\mathrm{12}}\:\: \\ $$$${t}_{\mathrm{4}} .............. \\ $$$${t}_{\mathrm{5}..............} \\ $$$${t}_{\mathrm{2022}} \:=\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2022}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2023}^{\mathrm{2}} }} \\ $$$${S}_{\mathrm{1}} \:=\:{t}_{\mathrm{1}} =\:\frac{\mathrm{3}}{\mathrm{2}}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{1}\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${S}_{\mathrm{2}} \:=\:{S}_{\mathrm{1}} +{t}_{\mathrm{2}} =\:\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{7}}{\mathrm{6}}=\:\frac{\mathrm{16}}{\mathrm{6}}\:=\frac{\mathrm{8}}{\mathrm{3}}=\mathrm{2}+\frac{\mathrm{2}}{\mathrm{3}}=\mathrm{2}\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${S}_{\mathrm{3}} \:=\:{S}_{\mathrm{2}} +{t}_{\mathrm{3}} \:=\:\frac{\mathrm{8}}{\mathrm{3}}+\frac{\mathrm{13}}{\mathrm{12}}=\:\frac{\mathrm{45}}{\mathrm{12}}=\frac{\mathrm{15}}{\mathrm{4}}=\mathrm{3}+\frac{\mathrm{3}}{\mathrm{4}}\:=\:\mathrm{3}\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${S}_{\mathrm{4}..........} \\ $$$${S}_{\mathrm{2022}} \:=\:\mathrm{2022}+\frac{\mathrm{2022}}{\mathrm{2023}}\:=\:\begin{array}{|c|}{\mathrm{2022}\frac{\mathrm{2022}}{\mathrm{2023}}}\\\hline\end{array}\mathrm{Answer} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com