Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 46573 by Rio Michael last updated on 28/Oct/18

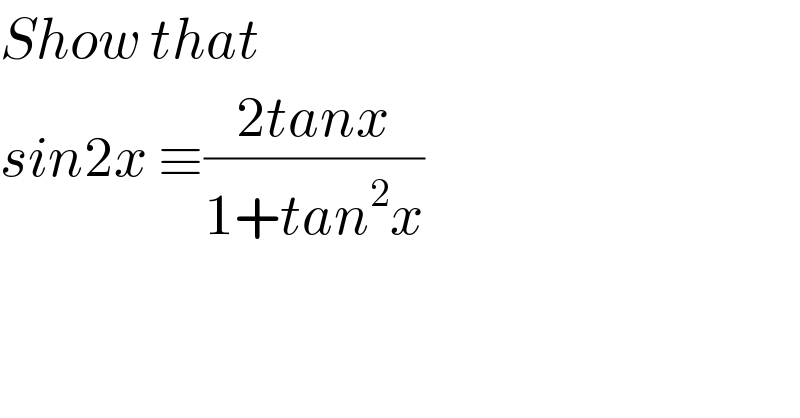
Show that sin2x ≡((2tanx)/(1+tan^2 x))

$${Show}\:{that}\: \\ $$$${sin}\mathrm{2}{x}\:\equiv\frac{\mathrm{2}{tanx}}{\mathrm{1}+{tan}^{\mathrm{2}} {x}} \\ $$

Commented by peter frank last updated on 28/Oct/18

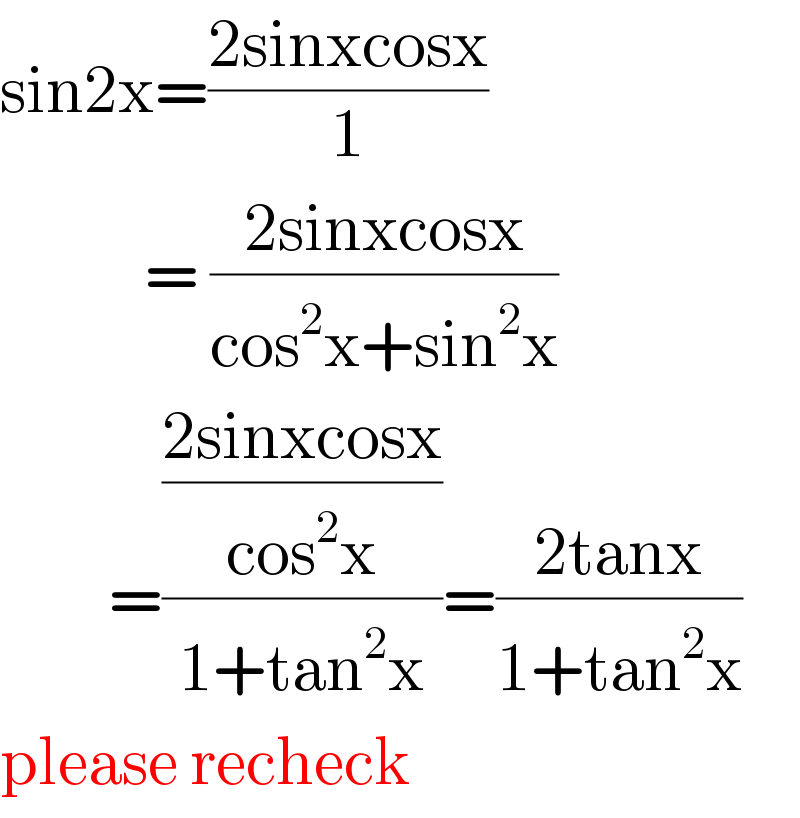
sin2x=((2sinxcosx)/1) = ((2sinxcosx)/(cos^2 x+sin^2 x)) =(((2sinxcosx)/(cos^2 x))/(1+tan^2 x))=((2tanx)/(1+tan^2 x)) please recheck

$$\mathrm{sin2x}=\frac{\mathrm{2sinxcosx}}{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{2sinxcosx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\frac{\mathrm{2sinxcosx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}}=\frac{\mathrm{2tanx}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}} \\ $$$$\mathrm{please}\:\mathrm{recheck} \\ $$

Commented by maxmathsup by imad last updated on 28/Oct/18

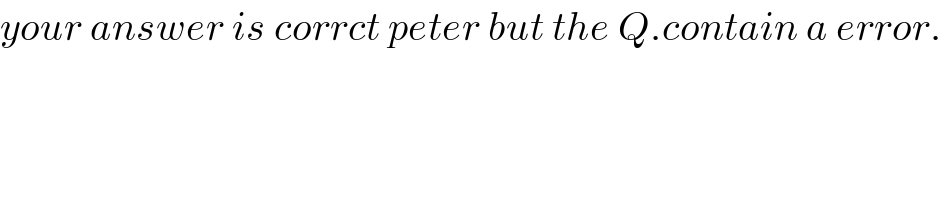
your answer is corrct peter but the Q.contain a error.

$${your}\:{answer}\:{is}\:{corrct}\:{peter}\:{but}\:{the}\:{Q}.{contain}\:{a}\:{error}. \\ $$

Commented by peter frank last updated on 28/Oct/18

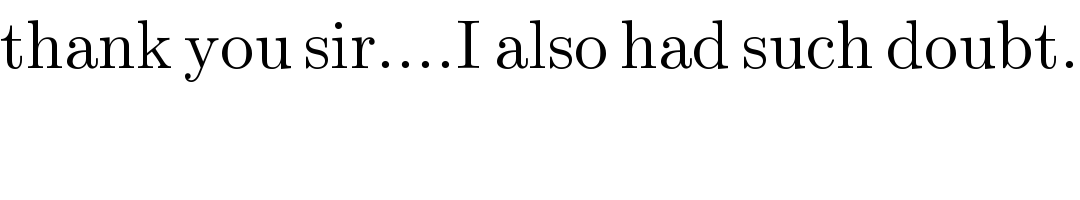
thank you sir....I also had such doubt.

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}....\mathrm{I}\:\mathrm{also}\:\mathrm{had}\:\mathrm{such}\:\mathrm{doubt}. \\ $$

Commented by hknkrc46 last updated on 29/Nov/18

tan 2x=((2tan x)/(1−tan^2 x))⇒2tan x=tan 2x(1−tan^2 x) {1−tan^2 x=1−((sin^2 x)/(cos^2 x))=((cos^2 x−sin^2 x)/(cos^2 x))=((cos 2x)/(cos^2 x))} 2tan x=tan 2x∙((cos 2x)/(cos^2 x))=((sin 2x)/(cos 2x))∙((cos 2x)/(cos^2 x))=((sin 2x)/(cos^2 x)) {1+tan^2 x=1+((sin^2 x)/(cos^2 x))=((sin^2 x+cos^2 x)/(cos^2 x))=(1/(cos^2 x))} ((2tan x)/(1+tan^2 x))=(((sin 2x)/(cos^2 x))/(1/(cos^2 x)))=sin 2x

$$\mathrm{tan}\:\mathrm{2}{x}=\frac{\mathrm{2tan}\:{x}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} {x}}\Rightarrow\mathrm{2tan}\:{x}=\mathrm{tan}\:\mathrm{2}{x}\left(\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} {x}\right) \\ $$$$\left\{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} {x}=\mathrm{1}−\frac{\mathrm{sin}\:^{\mathrm{2}} {x}}{\mathrm{cos}\:^{\mathrm{2}} {x}}=\frac{\mathrm{cos}\:^{\mathrm{2}} {x}−\mathrm{sin}\:^{\mathrm{2}} {x}}{\mathrm{cos}\:^{\mathrm{2}} {x}}=\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{cos}\:^{\mathrm{2}} {x}}\right\} \\ $$$$\mathrm{2tan}\:{x}=\mathrm{tan}\:\mathrm{2}{x}\centerdot\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{cos}\:^{\mathrm{2}} {x}}=\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{cos}\:\mathrm{2}{x}}\centerdot\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{cos}\:^{\mathrm{2}} {x}}=\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{cos}\:^{\mathrm{2}} {x}} \\ $$$$\left\{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}=\mathrm{1}+\frac{\mathrm{sin}\:^{\mathrm{2}} {x}}{\mathrm{cos}\:^{\mathrm{2}} {x}}=\frac{\mathrm{sin}\:^{\mathrm{2}} {x}+\mathrm{cos}\:^{\mathrm{2}} {x}}{\mathrm{cos}\:^{\mathrm{2}} {x}}=\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} {x}}\right\} \\ $$$$\frac{\mathrm{2tan}\:{x}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}}=\frac{\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{cos}\:^{\mathrm{2}} {x}}}{\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} {x}}}=\mathrm{sin}\:\mathrm{2}{x} \\ $$

Answered by Nabraj Awasthi last updated on 30/Oct/18

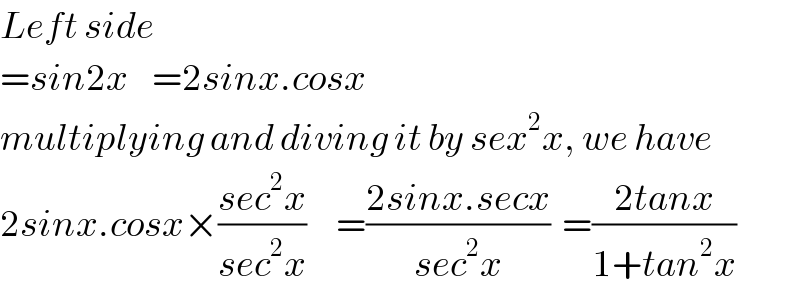
Left side =sin2x =2sinx.cosx multiplying and diving it by sex^2 x, we have 2sinx.cosx×((sec^2 x)/(sec^2 x)) =((2sinx.secx)/(sec^2 x)) =((2tanx)/(1+tan^2 x))

$${Left}\:{side} \\ $$$$={sin}\mathrm{2}{x}\:\:\:\:=\mathrm{2}{sinx}.{cosx} \\ $$$${multiplying}\:{and}\:{diving}\:{it}\:{by}\:{sex}^{\mathrm{2}} {x},\:{we}\:{have} \\ $$$$\mathrm{2}{sinx}.{cosx}×\frac{{sec}^{\mathrm{2}} {x}}{{sec}^{\mathrm{2}} {x}}\:\:\:\:\:=\frac{\mathrm{2}{sinx}.{secx}}{{sec}^{\mathrm{2}} {x}}\:\:=\frac{\mathrm{2}{tanx}}{\mathrm{1}+{tan}^{\mathrm{2}} {x}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com