
Question Number 13904 by tawa tawa last updated on 24/May/17
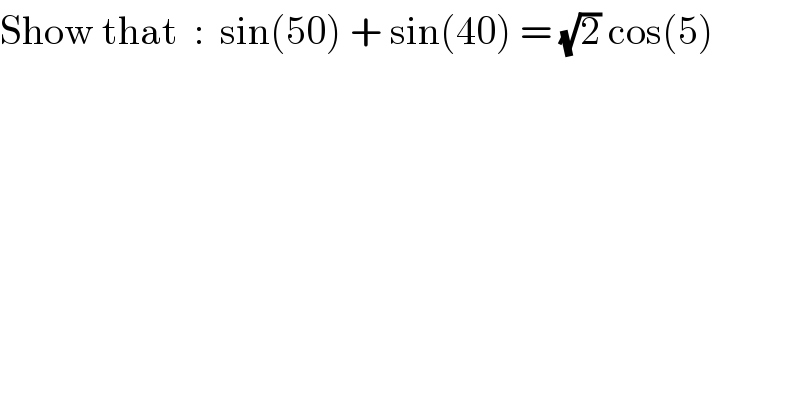
$$\mathrm{Show}\:\mathrm{that}\:\::\:\:\mathrm{sin}\left(\mathrm{50}\right)\:+\:\mathrm{sin}\left(\mathrm{40}\right)\:=\:\sqrt{\mathrm{2}}\:\mathrm{cos}\left(\mathrm{5}\right) \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 25/May/17
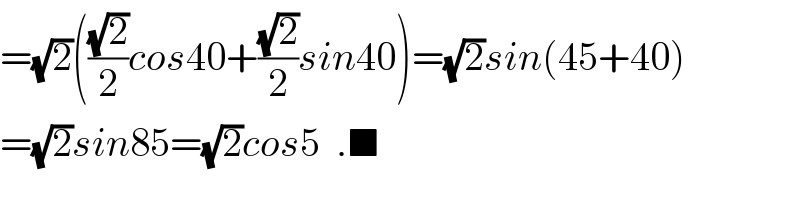
$$=\sqrt{\mathrm{2}}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{cos}\mathrm{40}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{sin}\mathrm{40}\right)=\sqrt{\mathrm{2}}{sin}\left(\mathrm{45}+\mathrm{40}\right) \\ $$$$=\sqrt{\mathrm{2}}{sin}\mathrm{85}=\sqrt{\mathrm{2}}{cos}\mathrm{5}\:\:.\blacksquare \\ $$
Commented by tawa tawa last updated on 25/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by Tinkutara last updated on 25/May/17
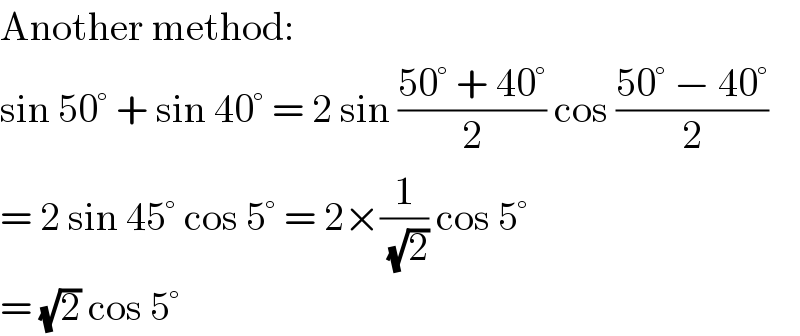
$$\mathrm{Another}\:\mathrm{method}: \\ $$$$\mathrm{sin}\:\mathrm{50}°\:+\:\mathrm{sin}\:\mathrm{40}°\:=\:\mathrm{2}\:\mathrm{sin}\:\frac{\mathrm{50}°\:+\:\mathrm{40}°}{\mathrm{2}}\:\mathrm{cos}\:\frac{\mathrm{50}°\:−\:\mathrm{40}°}{\mathrm{2}} \\ $$$$=\:\mathrm{2}\:\mathrm{sin}\:\mathrm{45}°\:\mathrm{cos}\:\mathrm{5}°\:=\:\mathrm{2}×\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\mathrm{cos}\:\mathrm{5}° \\ $$$$=\:\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{5}° \\ $$
Commented by tawa tawa last updated on 25/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
