Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 197184 by pete last updated on 10/Sep/23

Show that log(−logi)=log((π/2))−i(π/2)

$$\mathrm{Show}\:\mathrm{that}\:\mathrm{log}\left(−\mathrm{log}{i}\right)=\mathrm{log}\left(\frac{\pi}{\mathrm{2}}\right)−{i}\frac{\pi}{\mathrm{2}} \\ $$

Answered by Frix last updated on 10/Sep/23

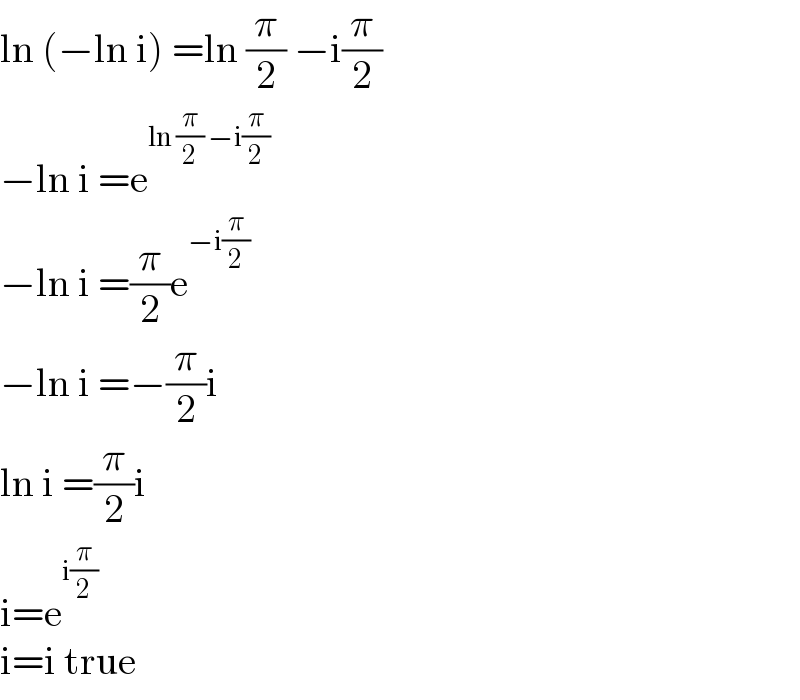
ln (−ln i) =ln (π/2) −i(π/2) −ln i =e^(ln (π/2) −i(π/2)) −ln i =(π/2)e^(−i(π/2)) −ln i =−(π/2)i ln i =(π/2)i i=e^(i(π/2)) i=i true

$$\mathrm{ln}\:\left(−\mathrm{ln}\:\mathrm{i}\right)\:=\mathrm{ln}\:\frac{\pi}{\mathrm{2}}\:−\mathrm{i}\frac{\pi}{\mathrm{2}} \\ $$$$−\mathrm{ln}\:\mathrm{i}\:=\mathrm{e}^{\mathrm{ln}\:\frac{\pi}{\mathrm{2}}\:−\mathrm{i}\frac{\pi}{\mathrm{2}}} \\ $$$$−\mathrm{ln}\:\mathrm{i}\:=\frac{\pi}{\mathrm{2}}\mathrm{e}^{−\mathrm{i}\frac{\pi}{\mathrm{2}}} \\ $$$$−\mathrm{ln}\:\mathrm{i}\:=−\frac{\pi}{\mathrm{2}}\mathrm{i} \\ $$$$\mathrm{ln}\:\mathrm{i}\:=\frac{\pi}{\mathrm{2}}\mathrm{i} \\ $$$$\mathrm{i}=\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{2}}} \\ $$$$\mathrm{i}=\mathrm{i}\:\mathrm{true} \\ $$

Commented by pete last updated on 10/Sep/23

Thank you sir

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by Frix last updated on 10/Sep/23

��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com