Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 82073 by TawaTawa last updated on 18/Feb/20

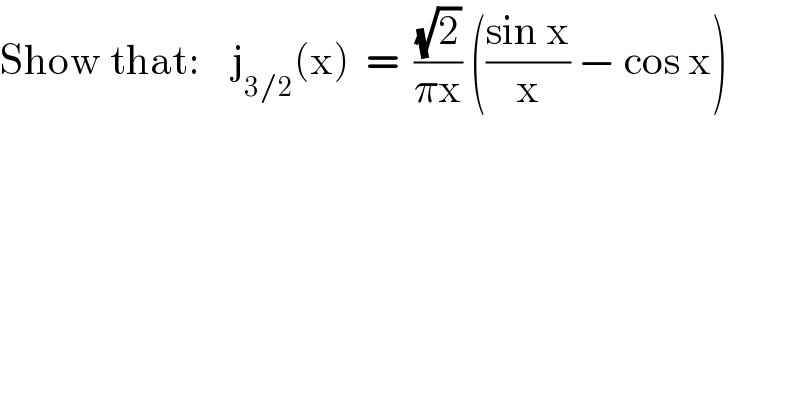
Show that: j_(3/2) (x) = ((√2)/(πx)) (((sin x)/x) − cos x)

$$\mathrm{Show}\:\mathrm{that}:\:\:\:\:\mathrm{j}_{\mathrm{3}/\mathrm{2}} \left(\mathrm{x}\right)\:\:=\:\:\frac{\sqrt{\mathrm{2}}}{\pi\mathrm{x}}\:\left(\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\:−\:\mathrm{cos}\:\mathrm{x}\right) \\ $$

Commented by jagoll last updated on 18/Feb/20

what is j_(3/2) ?

$${what}\:{is}\:{j}_{\frac{\mathrm{3}}{\mathrm{2}}} ? \\ $$

Commented by TawaTawa last updated on 18/Feb/20

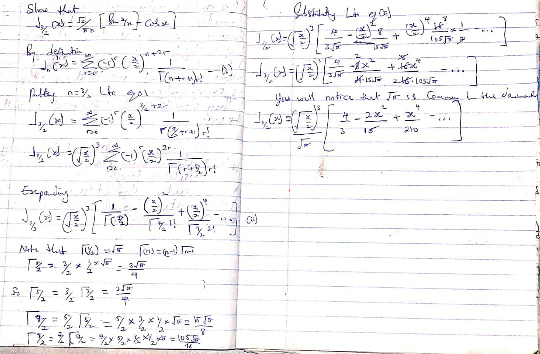
Commented by TawaTawa last updated on 18/Feb/20

Am lost here.

$$\mathrm{Am}\:\mathrm{lost}\:\mathrm{here}. \\ $$

Answered by mind is power last updated on 18/Feb/20

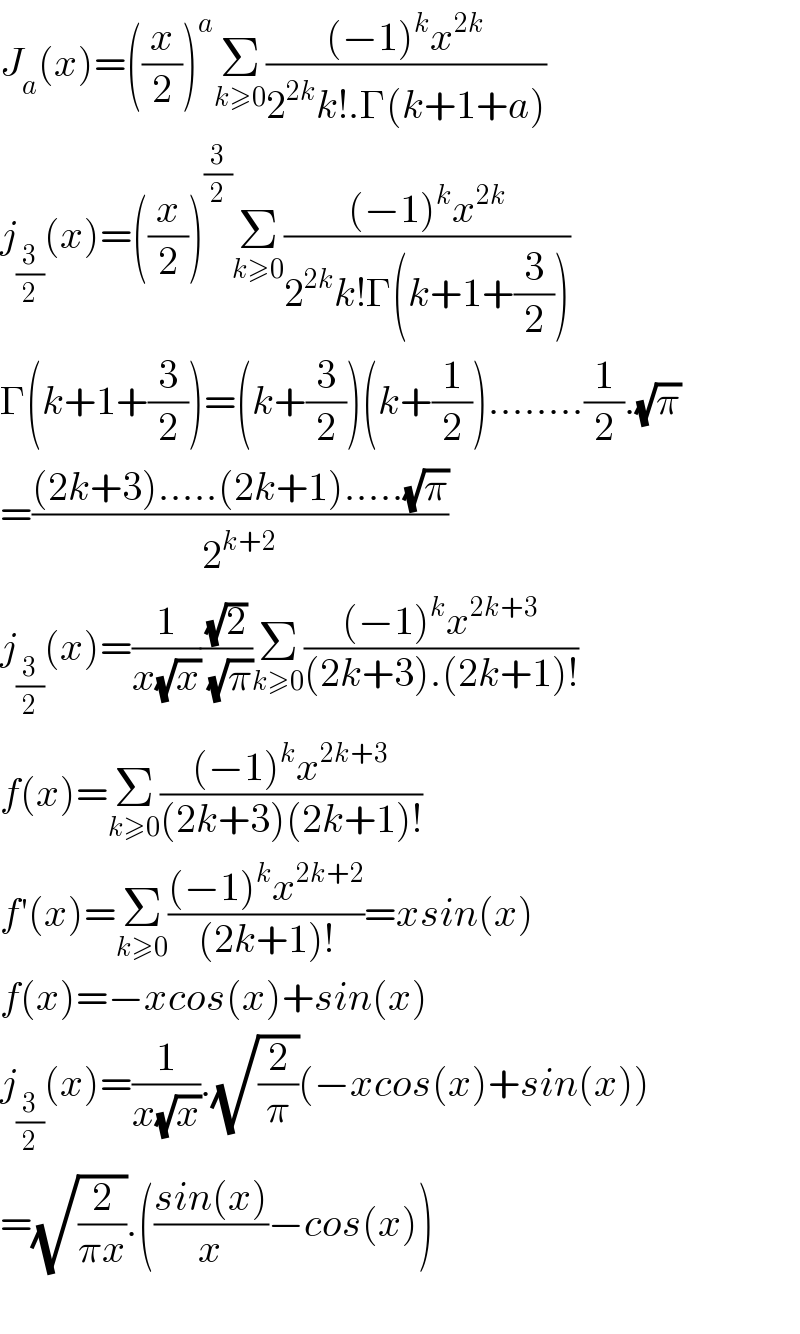
J_a (x)=((x/2))^a Σ_(k≥0) (((−1)^k x^(2k) )/(2^(2k) k!.Γ(k+1+a))) j_(3/2) (x)=((x/2))^(3/2) Σ_(k≥0) (((−1)^k x^(2k) )/(2^(2k) k!Γ(k+1+(3/2)))) Γ(k+1+(3/2))=(k+(3/2))(k+(1/2))........(1/2).(√π) =(((2k+3).....(2k+1).....(√π))/2^(k+2) ) j_(3/2) (x)=(1/(x(√x)))((√2)/(√π))Σ_(k≥0) (((−1)^k x^(2k+3) )/((2k+3).(2k+1)!)) f(x)=Σ_(k≥0) (((−1)^k x^(2k+3) )/((2k+3)(2k+1)!)) f′(x)=Σ_(k≥0) (((−1)^k x^(2k+2) )/((2k+1)!))=xsin(x) f(x)=−xcos(x)+sin(x) j_(3/2) (x)=(1/(x(√x))).(√(2/π))(−xcos(x)+sin(x)) =(√(2/(πx))).(((sin(x))/x)−cos(x))

$${J}_{{a}} \left({x}\right)=\left(\frac{{x}}{\mathrm{2}}\right)^{{a}} \underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{\mathrm{2}{k}} }{\mathrm{2}^{\mathrm{2}{k}} {k}!.\Gamma\left({k}+\mathrm{1}+{a}\right)} \\ $$$${j}_{\frac{\mathrm{3}}{\mathrm{2}}} \left({x}\right)=\left(\frac{{x}}{\mathrm{2}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{\mathrm{2}{k}} }{\mathrm{2}^{\mathrm{2}{k}} {k}!\Gamma\left({k}+\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$$$\Gamma\left({k}+\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}\right)=\left({k}+\frac{\mathrm{3}}{\mathrm{2}}\right)\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)........\frac{\mathrm{1}}{\mathrm{2}}.\sqrt{\pi} \\ $$$$=\frac{\left(\mathrm{2}{k}+\mathrm{3}\right).....\left(\mathrm{2}{k}+\mathrm{1}\right).....\sqrt{\pi}}{\mathrm{2}^{{k}+\mathrm{2}} } \\ $$$${j}_{\frac{\mathrm{3}}{\mathrm{2}}} \left({x}\right)=\frac{\mathrm{1}}{{x}\sqrt{{x}}}\frac{\sqrt{\mathrm{2}}}{\sqrt{\pi}}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{\mathrm{2}{k}+\mathrm{3}} }{\left(\mathrm{2}{k}+\mathrm{3}\right).\left(\mathrm{2}{k}+\mathrm{1}\right)!} \\ $$$${f}\left({x}\right)=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{\mathrm{2}{k}+\mathrm{3}} }{\left(\mathrm{2}{k}+\mathrm{3}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)!} \\ $$$${f}'\left({x}\right)=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{\mathrm{2}{k}+\mathrm{2}} }{\left(\mathrm{2}{k}+\mathrm{1}\right)!}={xsin}\left({x}\right) \\ $$$${f}\left({x}\right)=−{xcos}\left({x}\right)+{sin}\left({x}\right) \\ $$$${j}_{\frac{\mathrm{3}}{\mathrm{2}}} \left({x}\right)=\frac{\mathrm{1}}{{x}\sqrt{{x}}}.\sqrt{\frac{\mathrm{2}}{\pi}}\left(−{xcos}\left({x}\right)+{sin}\left({x}\right)\right) \\ $$$$=\sqrt{\frac{\mathrm{2}}{\pi{x}}}.\left(\frac{{sin}\left({x}\right)}{{x}}−{cos}\left({x}\right)\right) \\ $$$$ \\ $$

Commented by TawaTawa last updated on 18/Feb/20

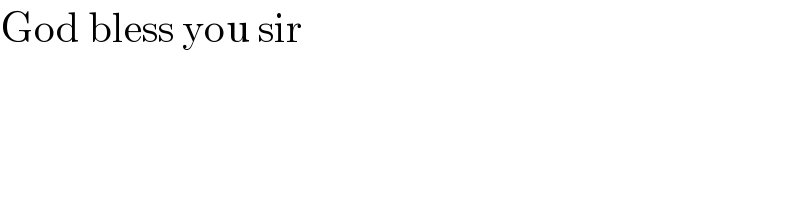
God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by mind is power last updated on 18/Feb/20

thanx miss you too

$${thanx}\:{miss}\:{you}\:{too}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com