
Question Number 80974 by Rio Michael last updated on 08/Feb/20
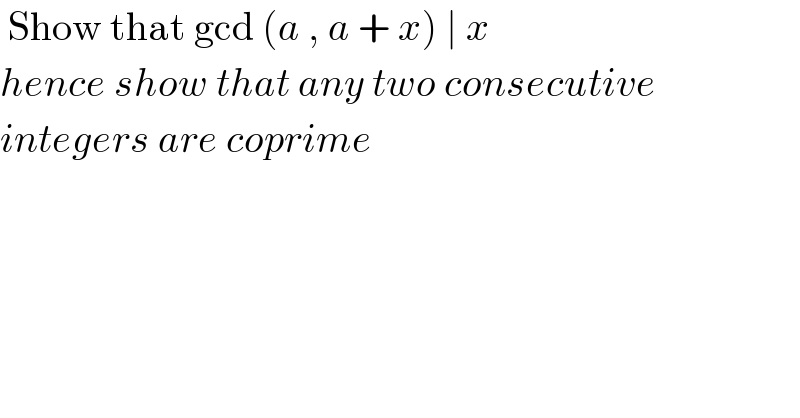
$$\:\mathrm{Show}\:\mathrm{that}\:\mathrm{gcd}\:\left({a}\:,\:{a}\:+\:{x}\right)\:\mid\:{x} \\ $$$${hence}\:{show}\:{that}\:{any}\:{two}\:{consecutive} \\ $$$${integers}\:{are}\:{coprime} \\ $$
Commented by kaivan.ahmadi last updated on 09/Feb/20
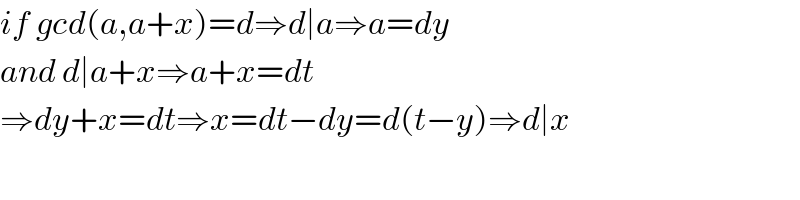
$${if}\:{gcd}\left({a},{a}+{x}\right)={d}\Rightarrow{d}\mid{a}\Rightarrow{a}={dy} \\ $$$${and}\:{d}\mid{a}+{x}\Rightarrow{a}+{x}={dt} \\ $$$$\Rightarrow{dy}+{x}={dt}\Rightarrow{x}={dt}−{dy}={d}\left({t}−{y}\right)\Rightarrow{d}\mid{x} \\ $$
Commented by Rio Michael last updated on 09/Feb/20

$${thanks} \\ $$
