
Question Number 185278 by Mastermind last updated on 19/Jan/23

$$\mathrm{Show}\:\mathrm{that}\:\mathrm{f}\left(\mathrm{z}\right)=\mathrm{z}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{harmonic}\:\mathrm{in} \\ $$$$\mathrm{polar}\:\mathrm{form} \\ $$
Commented by Frix last updated on 19/Jan/23

$$\mathrm{Please}\:\mathrm{tell}\:\mathrm{us}\:\mathrm{the}\:\mathrm{definition}\:\mathrm{of}\:\mathrm{a}\:``\mathrm{harmonic} \\ $$$$\mathrm{function}''\:\mathrm{in}\:\mathrm{complex}\:\mathrm{analysis}. \\ $$
Commented by Mastermind last updated on 19/Jan/23

$$\mathrm{Harmonic}\:\mathrm{function}\:\mathrm{is}\:\mathrm{any}\:\mathrm{function} \\ $$$$\mathrm{which}\:\mathrm{satisfies}\:\mathrm{Laplace}'\mathrm{s}\:\mathrm{equation} \\ $$
Commented by MJS_new last updated on 19/Jan/23
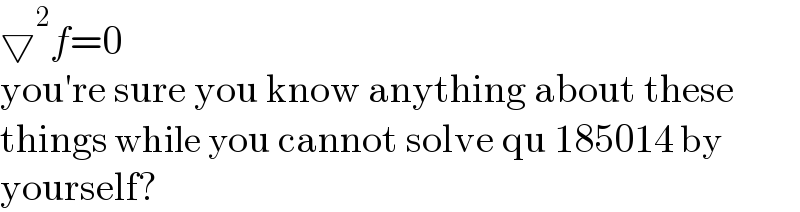
$$\bigtriangledown^{\mathrm{2}} {f}=\mathrm{0} \\ $$$$\mathrm{you}'\mathrm{re}\:\mathrm{sure}\:\mathrm{you}\:\mathrm{know}\:\mathrm{anything}\:\mathrm{about}\:\mathrm{these} \\ $$$$\mathrm{things}\:\mathrm{while}\:\mathrm{you}\:\mathrm{cannot}\:\mathrm{solve}\:\mathrm{qu}\:\mathrm{185014}\:\mathrm{by} \\ $$$$\mathrm{yourself}? \\ $$
Answered by 123564 last updated on 19/Jan/23

