Question and Answers Forum

All Questions      Topic List

Probability and Statistics Questions

Previous in All Question      Next in All Question      

Previous in Probability and Statistics      Next in Probability and Statistics      

Question Number 192375 by Spillover last updated on 16/May/23

Show that E(Z)=0 and Var(Z)=1 where Z is the standard normal variable

$${Show}\:{that}\:{E}\left({Z}\right)=\mathrm{0}\:\:\:{and}\:{Var}\left({Z}\right)=\mathrm{1}\:{where} \\ $$$${Z}\:{is}\:{the}\:{standard}\:{normal}\:{variable} \\ $$

Answered by mehdee42 last updated on 16/May/23

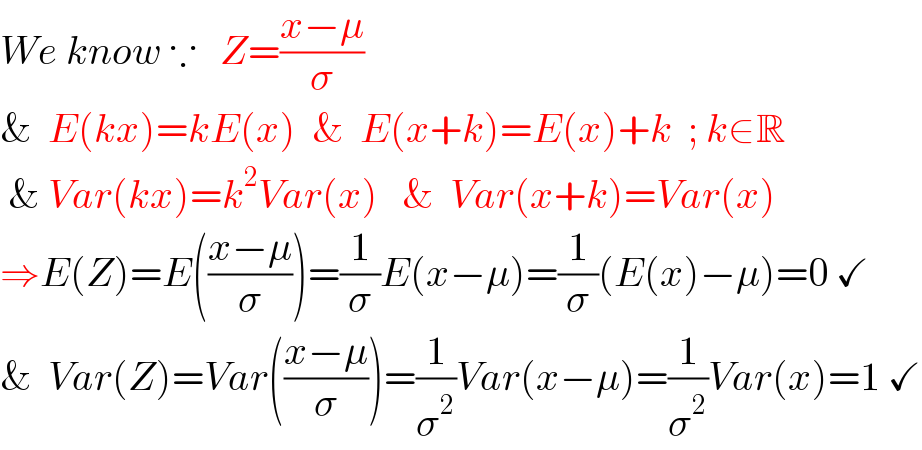
We know ∵ Z=((x−μ)/σ) & E(kx)=kE(x) & E(x+k)=E(x)+k ; k∈R & Var(kx)=k^2 Var(x) & Var(x+k)=Var(x) ⇒E(Z)=E(((x−μ)/σ))=(1/σ)E(x−μ)=(1/σ)(E(x)−μ)=0 ✓ & Var(Z)=Var(((x−μ)/σ))=(1/σ^2 )Var(x−μ)=(1/σ^2 )Var(x)=1 ✓

$${We}\:{know}\:\because\:\:\:{Z}=\frac{{x}−\mu}{\sigma}\:\:\: \\ $$$$\&\:\:{E}\left({kx}\right)={kE}\left({x}\right)\:\:\&\:\:{E}\left({x}+{k}\right)={E}\left({x}\right)+{k}\:\:;\:{k}\in\mathbb{R} \\ $$$$\:\&\:{Var}\left({kx}\right)={k}^{\mathrm{2}} {Var}\left({x}\right)\:\:\:\&\:\:{Var}\left({x}+{k}\right)={Var}\left({x}\right) \\ $$$$\Rightarrow{E}\left({Z}\right)={E}\left(\frac{{x}−\mu}{\sigma}\right)=\frac{\mathrm{1}}{\sigma}{E}\left({x}−\mu\right)=\frac{\mathrm{1}}{\sigma}\left({E}\left({x}\right)−\mu\right)=\mathrm{0}\:\checkmark \\ $$$$\&\:\:{Var}\left({Z}\right)={Var}\left(\frac{{x}−\mu}{\sigma}\right)=\frac{\mathrm{1}}{\sigma^{\mathrm{2}} }{Var}\left({x}−\mu\right)=\frac{\mathrm{1}}{\sigma^{\mathrm{2}} }{Var}\left({x}\right)=\mathrm{1}\:\checkmark \\ $$

Commented by Spillover last updated on 17/May/23

thanks

$${thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com