Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 198828 by a.lgnaoui last updated on 24/Oct/23

Show that: Area(blue circle)=Area(Green circle)

$$\:\:\boldsymbol{\mathrm{Show}}\:\boldsymbol{\mathrm{th}{at}}: \\ $$$$\:\boldsymbol{{Area}}\left(\boldsymbol{{blue}}\:\boldsymbol{{circle}}\right)=\boldsymbol{{Area}}\left(\boldsymbol{{Green}}\:\:\boldsymbol{{circle}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Commented by a.lgnaoui last updated on 24/Oct/23

Answered by mr W last updated on 25/Oct/23

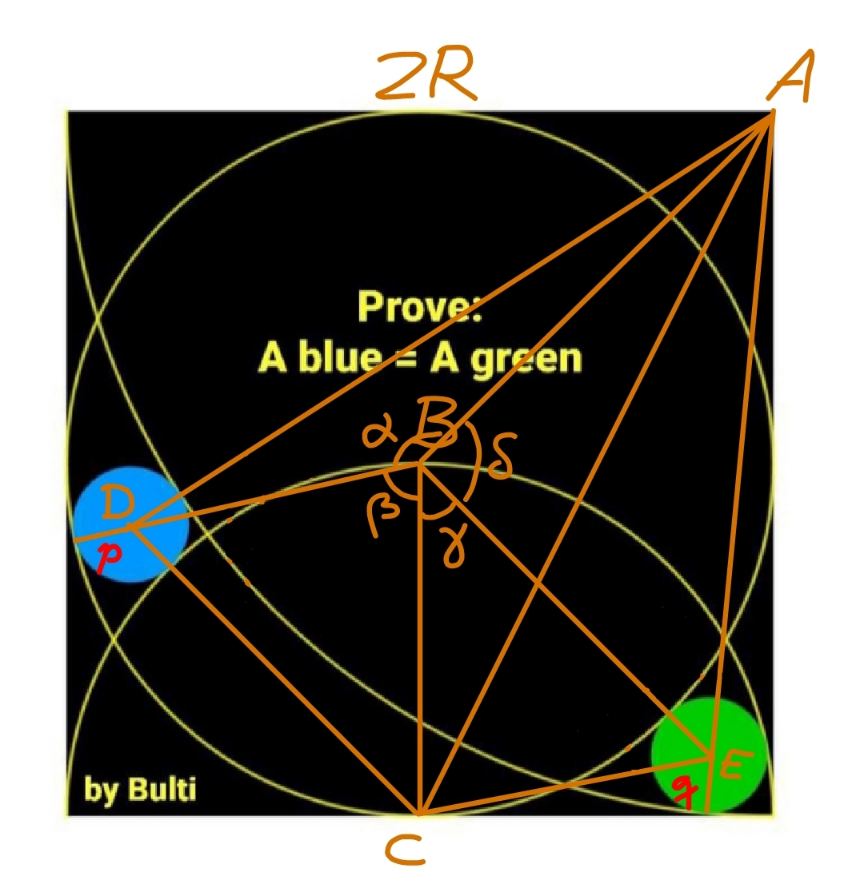
Commented by mr W last updated on 25/Oct/23

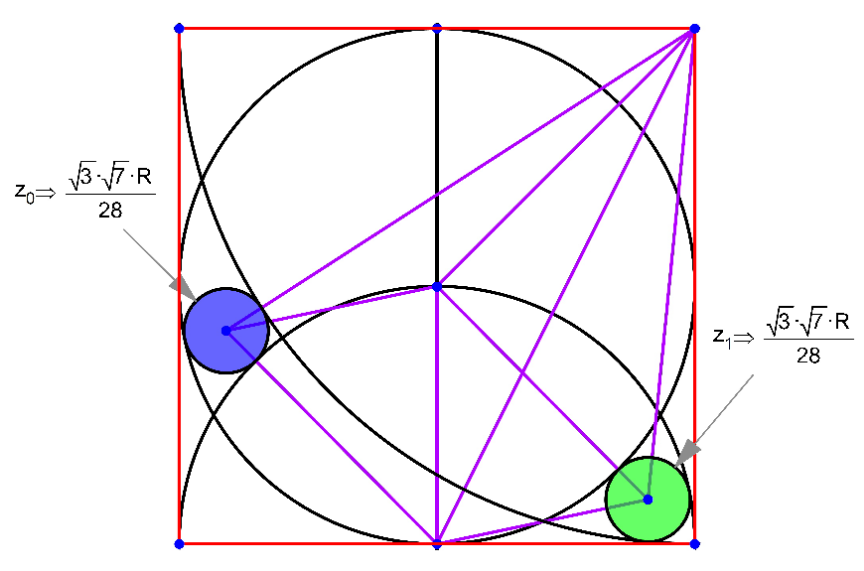
Commented by mr W last updated on 25/Oct/23

AD=2R+p BD=R−p CD=R+p AB=(√2)R BC=R AC=(√(R^2 +(2R)^2 ))=(√5)R cos α=((((√2)R)^2 +(R−p)^2 −(2R+p)^2 )/(2(√2)R(R−p))) =−((R+6p)/(2(√2)(R−p)))=−((1+6λ)/(2(√2)(1−λ))) with λ=(p/R) cos β=((R^2 +(R−p)^2 −(R+p)^2 )/(2R(R−p))) =((R−4p)/(2(R−p)))=((1−4λ)/(2(1−λ))) α+β=π+(π/4) cos (α+β)=−((√2)/2) −((√2)/2)=−((1+6λ)/(2(√2)(1−λ)))×((1−4λ)/(2(1−λ)))−((√(8(1−λ)^2 −(1+6λ)^2 ))/(2(√2)(1−λ)))×((√(4(1−λ)^2 −(1−4λ)^2 ))/(2(1−λ))) −((√2)/2)=((24λ^2 −2λ−1)/( 4(√2)(1−λ)^2 ))−((√(3(7−28λ−28λ^2 )(1−4λ^2 )))/( 4(√2)(1−λ)^2 )) 28λ^2 −10λ+3=(√(3(7−28λ−28λ^2 )(1−4λ^2 ))) 4(λ−1)^2 (112λ^2 −3)=0 ⇒λ=1 ⇒rejected ⇒112λ^2 =3 ⇒λ=(√(3/(112)))=((√(21))/(28)) ⇒p=(((√(21))R)/(28)) ✓ in similar way we can get q=(((√(21))R)/(28)). p=q=(((√(21))R)/(28)) ⇒blue circle=green circle

$${AD}=\mathrm{2}{R}+{p} \\ $$$${BD}={R}−{p} \\ $$$${CD}={R}+{p} \\ $$$${AB}=\sqrt{\mathrm{2}}{R} \\ $$$${BC}={R} \\ $$$${AC}=\sqrt{{R}^{\mathrm{2}} +\left(\mathrm{2}{R}\right)^{\mathrm{2}} }=\sqrt{\mathrm{5}}{R} \\ $$$$\mathrm{cos}\:\alpha=\frac{\left(\sqrt{\mathrm{2}}{R}\right)^{\mathrm{2}} +\left({R}−{p}\right)^{\mathrm{2}} −\left(\mathrm{2}{R}+{p}\right)^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{2}}{R}\left({R}−{p}\right)} \\ $$$$\:\:\:\:=−\frac{{R}+\mathrm{6}{p}}{\mathrm{2}\sqrt{\mathrm{2}}\left({R}−{p}\right)}=−\frac{\mathrm{1}+\mathrm{6}\lambda}{\mathrm{2}\sqrt{\mathrm{2}}\left(\mathrm{1}−\lambda\right)} \\ $$$${with}\:\lambda=\frac{{p}}{{R}} \\ $$$$\mathrm{cos}\:\beta=\frac{{R}^{\mathrm{2}} +\left({R}−{p}\right)^{\mathrm{2}} −\left({R}+{p}\right)^{\mathrm{2}} }{\mathrm{2}{R}\left({R}−{p}\right)} \\ $$$$\:\:\:\:=\frac{{R}−\mathrm{4}{p}}{\mathrm{2}\left({R}−{p}\right)}=\frac{\mathrm{1}−\mathrm{4}\lambda}{\mathrm{2}\left(\mathrm{1}−\lambda\right)} \\ $$$$\alpha+\beta=\pi+\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{cos}\:\left(\alpha+\beta\right)=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=−\frac{\mathrm{1}+\mathrm{6}\lambda}{\mathrm{2}\sqrt{\mathrm{2}}\left(\mathrm{1}−\lambda\right)}×\frac{\mathrm{1}−\mathrm{4}\lambda}{\mathrm{2}\left(\mathrm{1}−\lambda\right)}−\frac{\sqrt{\mathrm{8}\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} −\left(\mathrm{1}+\mathrm{6}\lambda\right)^{\mathrm{2}} }}{\mathrm{2}\sqrt{\mathrm{2}}\left(\mathrm{1}−\lambda\right)}×\frac{\sqrt{\mathrm{4}\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} −\left(\mathrm{1}−\mathrm{4}\lambda\right)^{\mathrm{2}} }}{\mathrm{2}\left(\mathrm{1}−\lambda\right)} \\ $$$$−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=\frac{\mathrm{24}\lambda^{\mathrm{2}} −\mathrm{2}\lambda−\mathrm{1}}{\:\mathrm{4}\sqrt{\mathrm{2}}\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} }−\frac{\sqrt{\mathrm{3}\left(\mathrm{7}−\mathrm{28}\lambda−\mathrm{28}\lambda^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{4}\lambda^{\mathrm{2}} \right)}}{\:\mathrm{4}\sqrt{\mathrm{2}}\left(\mathrm{1}−\lambda\right)^{\mathrm{2}} } \\ $$$$\mathrm{28}\lambda^{\mathrm{2}} −\mathrm{10}\lambda+\mathrm{3}=\sqrt{\mathrm{3}\left(\mathrm{7}−\mathrm{28}\lambda−\mathrm{28}\lambda^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{4}\lambda^{\mathrm{2}} \right)} \\ $$$$\mathrm{4}\left(\lambda−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{112}\lambda^{\mathrm{2}} −\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow\lambda=\mathrm{1}\:\Rightarrow{rejected} \\ $$$$\Rightarrow\mathrm{112}\lambda^{\mathrm{2}} =\mathrm{3}\:\Rightarrow\lambda=\sqrt{\frac{\mathrm{3}}{\mathrm{112}}}=\frac{\sqrt{\mathrm{21}}}{\mathrm{28}} \\ $$$$\Rightarrow{p}=\frac{\sqrt{\mathrm{21}}{R}}{\mathrm{28}}\:\checkmark \\ $$$${in}\:{similar}\:{way}\:{we}\:{can}\:{get}\:{q}=\frac{\sqrt{\mathrm{21}}{R}}{\mathrm{28}}. \\ $$$${p}={q}=\frac{\sqrt{\mathrm{21}}{R}}{\mathrm{28}}\: \\ $$$$\Rightarrow{blue}\:{circle}={green}\:{circle} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com