Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 136210 by Ar Brandon last updated on 19/Mar/21

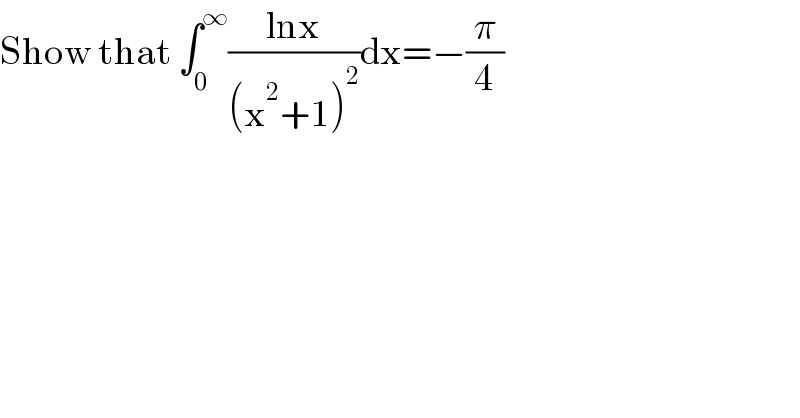
Show that ∫_0 ^∞ ((lnx)/((x^2 +1)^2 ))dx=−(π/4)

$$\mathrm{Show}\:\mathrm{that}\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}=−\frac{\pi}{\mathrm{4}} \\ $$

Commented by Ar Brandon last updated on 19/Mar/21

Oh ! Thank You Sir 😃

$$\mathrm{Oh}\:!\:\mathrm{Thank}\:\mathrm{You}\:\mathrm{Sir} \\ $$😃

Commented by Ar Brandon last updated on 19/Mar/21

Ω=∫_0 ^∞ ((lnx)/((x^2 +1)^2 ))dx =(∂/∂s)∣_(s=0) ∫_0 ^∞ (x^s /((x^2 +1)^2 ))dx=^(u=x^2 ) (∂/∂s)∣_(s=0) (1/2)∫_0 ^∞ (u^((s/2)−(1/2)) /((u+1)^2 ))du =(∂/∂s)∣_(s=0) (1/2)β((s/2)+(1/2), (3/2)−(s/2))=(∂/∂s)∣_(s=0) (1/2)Γ((s/2)+(1/2))Γ((3/2)−(s/2)) =(1/2)∣_(s=0) Γ((s/2)+(1/2))Γ′((3/2)−(s/2))+Γ((3/2)−(s/2))Γ′((s/2)+(1/2)) =(1/2)∙(1/2)Γ((1/2))Γ((3/2))[ψ((1/2))−ψ((3/2))]=(π/8)[ψ((1/2))−ψ((1/2))−2]=−(π/4)

$$\Omega=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\:\:\:\:\:=\frac{\partial}{\partial\mathrm{s}}\mid_{\mathrm{s}=\mathrm{0}} \int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{\mathrm{s}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\overset{\mathrm{u}=\mathrm{x}^{\mathrm{2}} } {=}\frac{\partial}{\partial\mathrm{s}}\mid_{\mathrm{s}=\mathrm{0}} \frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{\frac{\mathrm{s}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}} }{\left(\mathrm{u}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{du} \\ $$$$\:\:\:\:\:=\frac{\partial}{\partial\mathrm{s}}\mid_{\mathrm{s}=\mathrm{0}} \frac{\mathrm{1}}{\mathrm{2}}\beta\left(\frac{\mathrm{s}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}},\:\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{s}}{\mathrm{2}}\right)=\frac{\partial}{\partial\mathrm{s}}\mid_{\mathrm{s}=\mathrm{0}} \frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{s}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{s}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mid_{\mathrm{s}=\mathrm{0}} \Gamma\left(\frac{\mathrm{s}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma'\left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{s}}{\mathrm{2}}\right)+\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{s}}{\mathrm{2}}\right)\Gamma'\left(\frac{\mathrm{s}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\left[\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\right]=\frac{\pi}{\mathrm{8}}\left[\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2}\right]=−\frac{\pi}{\mathrm{4}} \\ $$

Commented by mnjuly1970 last updated on 19/Mar/21

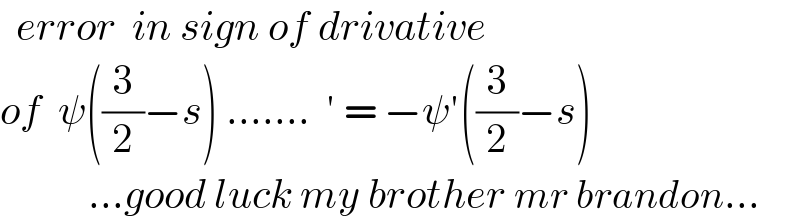
error in sign of drivative of ψ((3/2)−s) ....... ′ = −ψ′((3/2)−s) ...good luck my brother mr brandon...

$$\:\:{error}\:\:{in}\:{sign}\:{of}\:{drivative} \\ $$$${of}\:\:\psi\left(\frac{\mathrm{3}}{\mathrm{2}}−{s}\right)\:.......\:\:'\:=\:−\psi'\left(\frac{\mathrm{3}}{\mathrm{2}}−{s}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:...{good}\:{luck}\:{my}\:{brother}\:{mr}\:{brandon}... \\ $$

Answered by mnjuly1970 last updated on 19/Mar/21

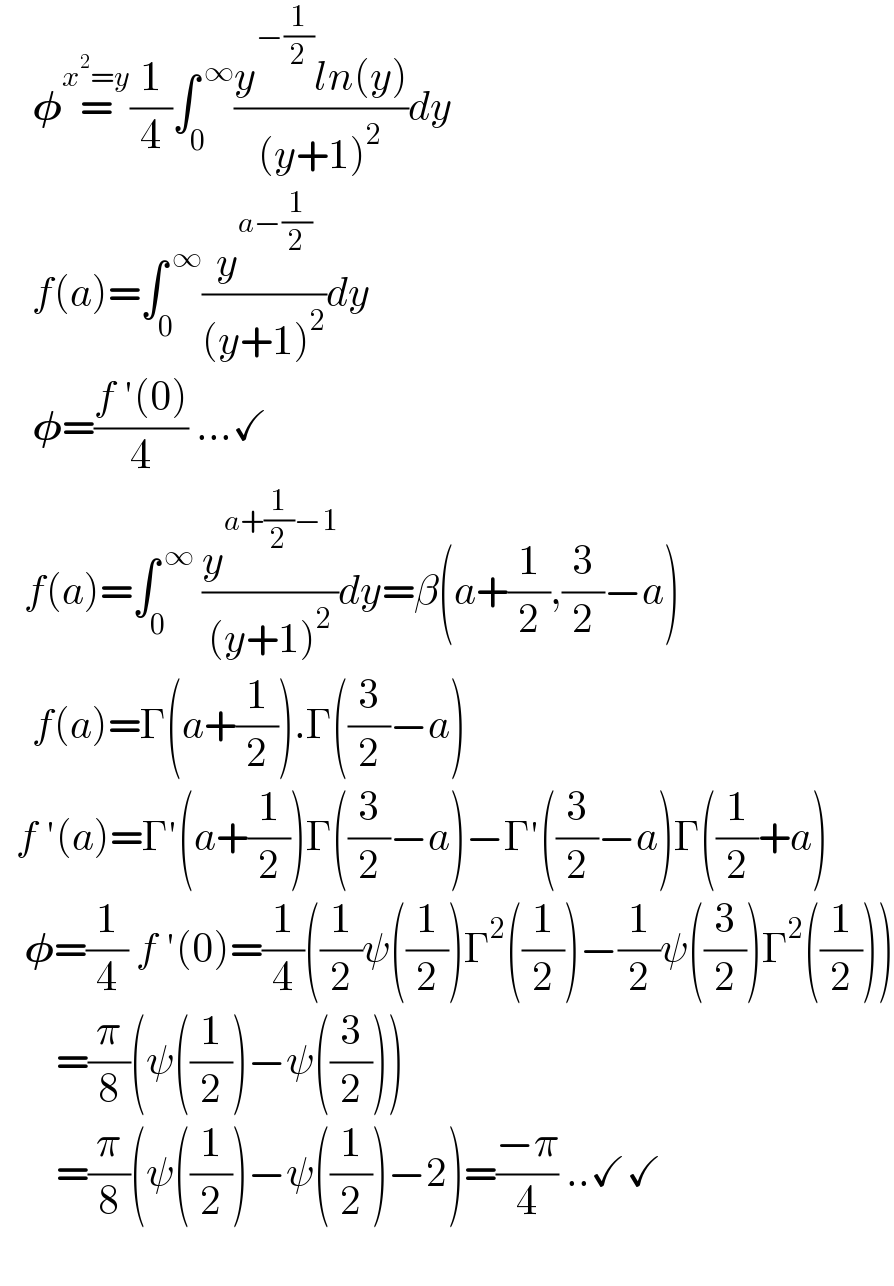
𝛗=^(x^2 =y) (1/4)∫_0 ^( ∞) ((y^(−(1/2)) ln(y))/((y+1)^2 ))dy f(a)=∫_0 ^( ∞) (y^(a−(1/2)) /((y+1)^2 ))dy 𝛗=((f ′(0))/4) ...✓ f(a)=∫_0 ^( ∞) (y^(a+(1/2)−1) /((y+1)^2 ))dy=β(a+(1/2),(3/2)−a) f(a)=Γ(a+(1/2)).Γ((3/2)−a) f ′(a)=Γ′(a+(1/2))Γ((3/2)−a)−Γ′((3/2)−a)Γ((1/2)+a) 𝛗=(1/4) f ′(0)=(1/4)((1/2)ψ((1/2))Γ^2 ((1/2))−(1/2)ψ((3/2))Γ^2 ((1/2))) =(π/8)(ψ((1/2))−ψ((3/2))) =(π/8)(ψ((1/2))−ψ((1/2))−2)=((−π)/4) ..✓✓

$$\:\:\:\:\boldsymbol{\phi}\overset{{x}^{\mathrm{2}} ={y}} {=}\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\infty} \frac{{y}^{−\frac{\mathrm{1}}{\mathrm{2}}} {ln}\left({y}\right)}{\left({y}+\mathrm{1}\right)^{\mathrm{2}} }{dy} \\ $$$$\:\:\:\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\:\infty} \frac{{y}^{{a}−\frac{\mathrm{1}}{\mathrm{2}}} }{\left({y}+\mathrm{1}\right)^{\mathrm{2}} }{dy} \\ $$$$\:\:\:\:\boldsymbol{\phi}=\frac{{f}\:'\left(\mathrm{0}\right)}{\mathrm{4}}\:...\checkmark \\ $$$$\:\:\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\:\infty} \:\frac{{y}^{{a}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} }{\left({y}+\mathrm{1}\right)^{\mathrm{2}} }{dy}=\beta\left({a}+\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}−{a}\right) \\ $$$$\:\:\:\:{f}\left({a}\right)=\Gamma\left({a}+\frac{\mathrm{1}}{\mathrm{2}}\right).\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}−{a}\right) \\ $$$$\:\:{f}\:'\left({a}\right)=\Gamma'\left({a}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}−{a}\right)−\Gamma'\left(\frac{\mathrm{3}}{\mathrm{2}}−{a}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}+{a}\right) \\ $$$$\:\:\:\boldsymbol{\phi}=\frac{\mathrm{1}}{\mathrm{4}}\:{f}\:'\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{2}}\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$\:\:\:\:\:\:\:=\frac{\pi}{\mathrm{8}}\left(\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\right) \\ $$$$\:\:\:\:\:\:\:=\frac{\pi}{\mathrm{8}}\left(\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2}\right)=\frac{−\pi}{\mathrm{4}}\:..\checkmark\checkmark \\ $$$$\:\: \\ $$

Answered by Dwaipayan Shikari last updated on 19/Mar/21

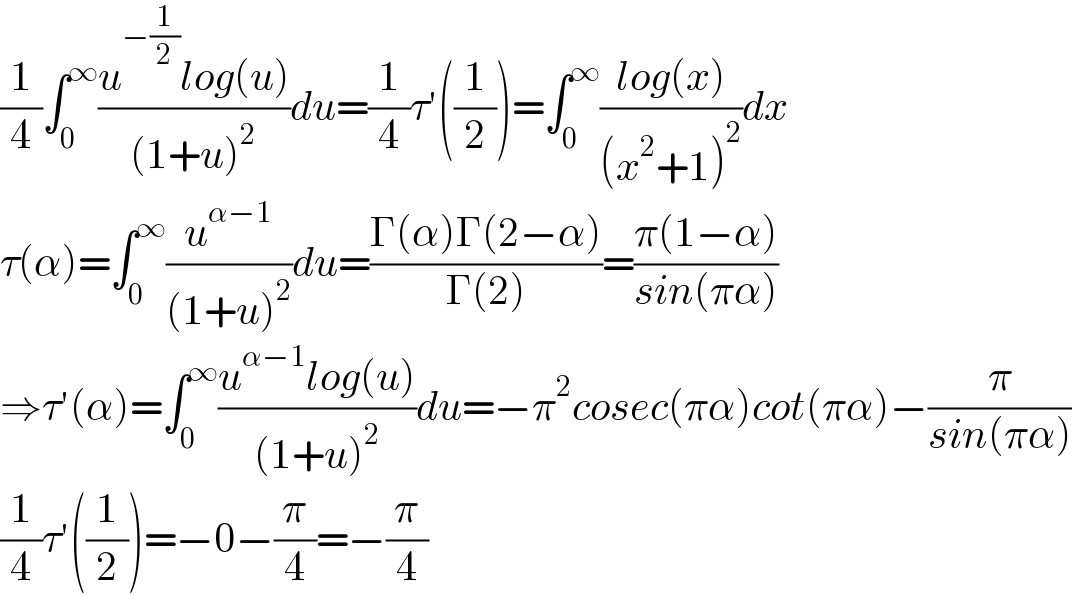
(1/4)∫_0 ^∞ ((u^(−(1/2)) log(u))/((1+u)^2 ))du=(1/4)τ′((1/2))=∫_0 ^∞ ((log(x))/((x^2 +1)^2 ))dx τ(α)=∫_0 ^∞ (u^(α−1) /((1+u)^2 ))du=((Γ(α)Γ(2−α))/(Γ(2)))=((π(1−α))/(sin(πα))) ⇒τ′(α)=∫_0 ^∞ ((u^(α−1) log(u))/((1+u)^2 ))du=−π^2 cosec(πα)cot(πα)−(π/(sin(πα))) (1/4)τ′((1/2))=−0−(π/4)=−(π/4)

$$\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} {log}\left({u}\right)}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }{du}=\frac{\mathrm{1}}{\mathrm{4}}\tau'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{log}\left({x}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\tau\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\alpha−\mathrm{1}} }{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }{du}=\frac{\Gamma\left(\alpha\right)\Gamma\left(\mathrm{2}−\alpha\right)}{\Gamma\left(\mathrm{2}\right)}=\frac{\pi\left(\mathrm{1}−\alpha\right)}{{sin}\left(\pi\alpha\right)} \\ $$$$\Rightarrow\tau'\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\alpha−\mathrm{1}} {log}\left({u}\right)}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }{du}=−\pi^{\mathrm{2}} {cosec}\left(\pi\alpha\right){cot}\left(\pi\alpha\right)−\frac{\pi}{{sin}\left(\pi\alpha\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\tau'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\mathrm{0}−\frac{\pi}{\mathrm{4}}=−\frac{\pi}{\mathrm{4}} \\ $$

Commented by Ar Brandon last updated on 19/Mar/21

Thanks bro

$$\mathrm{Thanks}\:\mathrm{bro} \\ $$

Commented by Dwaipayan Shikari last updated on 19/Mar/21

😃

$$ \\ $$😃

Answered by Ajetunmobi last updated on 19/Mar/21

i have drop the solution before here

$$ \\ $$$$\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{have}}\:\boldsymbol{\mathrm{drop}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{solution}}\:\boldsymbol{\mathrm{before}}\:\boldsymbol{\mathrm{here}} \\ $$

Commented by Ar Brandon last updated on 19/Mar/21

Alright ! Before posting I used the search option to check if it was previously posted but couldn′t find it. Thank You Sir

$$\mathrm{Alright}\:! \\ $$$$\mathrm{Before}\:\mathrm{posting}\:\mathrm{I}\:\mathrm{used}\:\mathrm{the}\:\mathrm{search}\:\mathrm{option}\: \\ $$$$\mathrm{to}\:\mathrm{check}\:\mathrm{if}\:\mathrm{it}\:\mathrm{was}\:\mathrm{previously}\:\mathrm{posted}\:\mathrm{but}\: \\ $$$$\mathrm{couldn}'\mathrm{t}\:\mathrm{find}\:\mathrm{it}.\:\mathrm{Thank}\:\mathrm{You}\:\mathrm{Sir} \\ $$

Commented by Ajetunmobi last updated on 19/Mar/21

ok

$$ \\ $$$$\boldsymbol{\mathrm{ok}} \\ $$

Answered by Ajetunmobi last updated on 19/Mar/21

Answered by mathmax by abdo last updated on 19/Mar/21

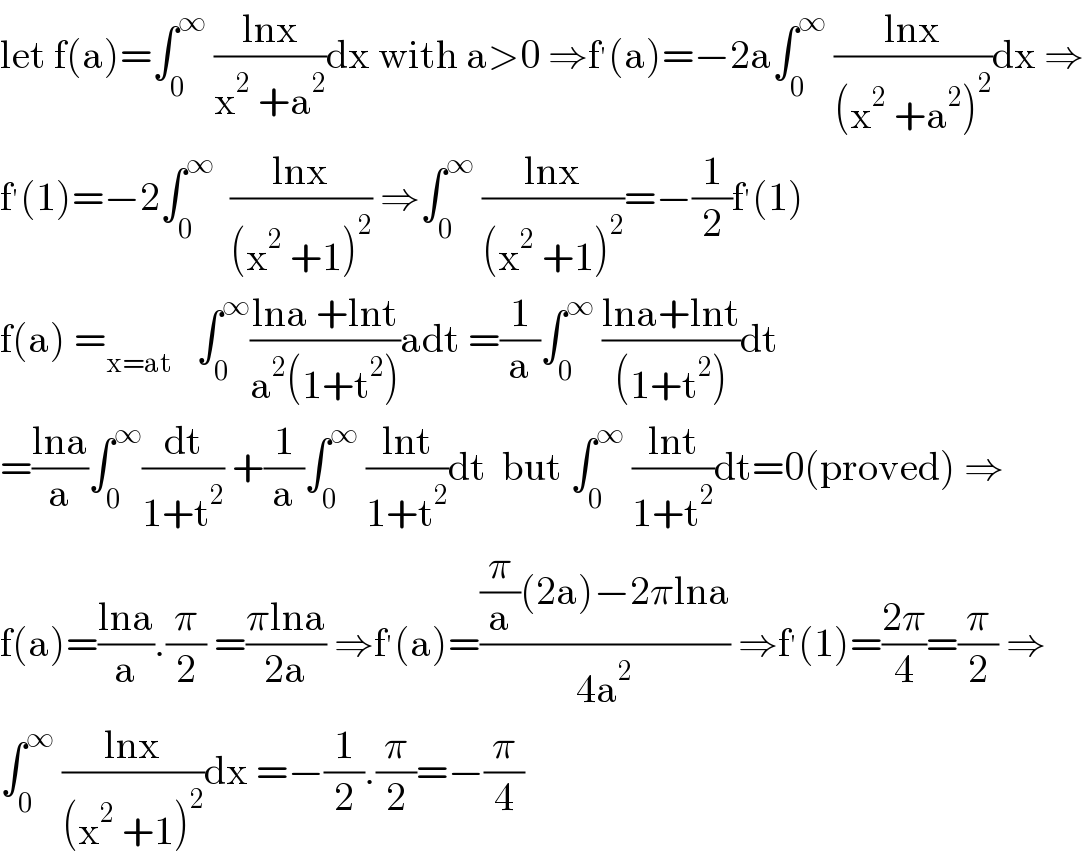
let f(a)=∫_0 ^∞ ((lnx)/(x^2 +a^2 ))dx with a>0 ⇒f^′ (a)=−2a∫_0 ^∞ ((lnx)/((x^2 +a^2 )^2 ))dx ⇒ f^′ (1)=−2∫_0 ^∞ ((lnx)/((x^2 +1)^2 )) ⇒∫_0 ^∞ ((lnx)/((x^2 +1)^2 ))=−(1/2)f^′ (1) f(a) =_(x=at) ∫_0 ^∞ ((lna +lnt)/(a^2 (1+t^2 )))adt =(1/a)∫_0 ^∞ ((lna+lnt)/((1+t^2 )))dt =((lna)/a)∫_0 ^∞ (dt/(1+t^2 )) +(1/a)∫_0 ^∞ ((lnt)/(1+t^2 ))dt but ∫_0 ^∞ ((lnt)/(1+t^2 ))dt=0(proved) ⇒ f(a)=((lna)/a).(π/2) =((πlna)/(2a)) ⇒f^′ (a)=(((π/a)(2a)−2πlna)/(4a^2 )) ⇒f^′ (1)=((2π)/4)=(π/2) ⇒ ∫_0 ^∞ ((lnx)/((x^2 +1)^2 ))dx =−(1/2).(π/2)=−(π/4)

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\mathrm{dx}\:\mathrm{with}\:\mathrm{a}>\mathrm{0}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=−\mathrm{2a}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{1}\right)=−\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{f}^{'} \left(\mathrm{1}\right) \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=_{\mathrm{x}=\mathrm{at}} \:\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{lna}\:+\mathrm{lnt}}{\mathrm{a}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\mathrm{adt}\:=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lna}+\mathrm{lnt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\mathrm{dt} \\ $$$$=\frac{\mathrm{lna}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:\:\mathrm{but}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}=\mathrm{0}\left(\mathrm{proved}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{\mathrm{lna}}{\mathrm{a}}.\frac{\pi}{\mathrm{2}}\:=\frac{\pi\mathrm{lna}}{\mathrm{2a}}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=\frac{\frac{\pi}{\mathrm{a}}\left(\mathrm{2a}\right)−\mathrm{2}\pi\mathrm{lna}}{\mathrm{4a}^{\mathrm{2}} }\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{1}\right)=\frac{\mathrm{2}\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi}{\mathrm{2}}=−\frac{\pi}{\mathrm{4}} \\ $$

Commented by mathmax by abdo last updated on 19/Mar/21

folow my facebook (abdo imad)

$$\mathrm{folow}\:\mathrm{my}\:\mathrm{facebook}\:\:\left(\mathrm{abdo}\:\mathrm{imad}\right) \\ $$

Commented by Ajetunmobi last updated on 19/Mar/21

sir mathmax by abdo how can we chat privately sir i need to talk about something with you you can send me your whatsapp number or your facebook name Thanks

$$ \\ $$$$\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{mathmax}}\:\boldsymbol{\mathrm{by}}\:\boldsymbol{\mathrm{abdo}} \\ $$$$\boldsymbol{\mathrm{how}}\:\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{chat}}\:\boldsymbol{\mathrm{privately}}\:\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{need}}\:\boldsymbol{\mathrm{to}} \\ $$$$\boldsymbol{\mathrm{talk}}\:\boldsymbol{\mathrm{about}}\:\boldsymbol{\mathrm{something}}\:\boldsymbol{\mathrm{with}}\:\boldsymbol{\mathrm{you}}\: \\ $$$$\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{send}}\:\boldsymbol{\mathrm{me}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{whatsapp}}\:\boldsymbol{\mathrm{number}} \\ $$$$\boldsymbol{\mathrm{or}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{facebook}}\:\boldsymbol{\mathrm{name}}\: \\ $$$$\boldsymbol{\mathrm{Thanks}} \\ $$

Commented by Ajetunmobi last updated on 20/Mar/21

there are many abdo imad there how will i recognize you sir?

$$ \\ $$$$\boldsymbol{\mathrm{there}}\:\boldsymbol{\mathrm{are}}\:\boldsymbol{\mathrm{many}}\:\boldsymbol{\mathrm{abdo}}\:\boldsymbol{\mathrm{imad}}\:\boldsymbol{\mathrm{there}}\: \\ $$$$\boldsymbol{\mathrm{how}}\:\boldsymbol{\mathrm{will}}\:\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{recognize}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{sir}}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com