Question and Answers Forum

All Questions      Topic List

Vector Calculus Questions

Previous in All Question      Next in All Question      

Previous in Vector Calculus      Next in Vector Calculus      

Question Number 119054 by mathocean1 last updated on 21/Oct/20

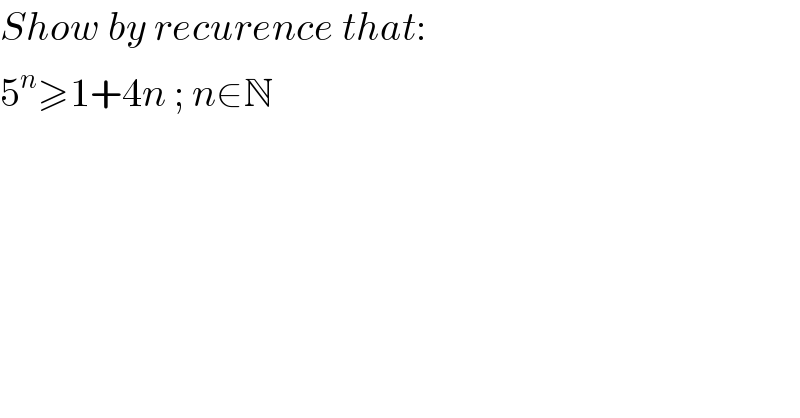
Show by recurence that: 5^n ≥1+4n ; n∈N

$${Show}\:{by}\:{recurence}\:{that}: \\ $$$$\mathrm{5}^{{n}} \geqslant\mathrm{1}+\mathrm{4}{n}\:;\:{n}\in\mathbb{N} \\ $$

Answered by 1549442205PVT last updated on 22/Oct/20

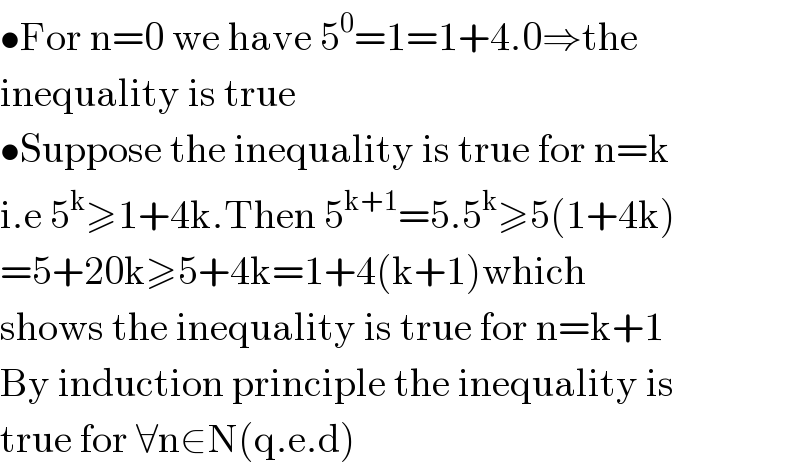
•For n=0 we have 5^0 =1=1+4.0⇒the inequality is true •Suppose the inequality is true for n=k i.e 5^k ≥1+4k.Then 5^(k+1) =5.5^k ≥5(1+4k) =5+20k≥5+4k=1+4(k+1)which shows the inequality is true for n=k+1 By induction principle the inequality is true for ∀n∈N(q.e.d)

$$\bullet\mathrm{For}\:\mathrm{n}=\mathrm{0}\:\mathrm{we}\:\mathrm{have}\:\mathrm{5}^{\mathrm{0}} =\mathrm{1}=\mathrm{1}+\mathrm{4}.\mathrm{0}\Rightarrow\mathrm{the} \\ $$$$\mathrm{inequality}\:\mathrm{is}\:\mathrm{true} \\ $$$$\bullet\mathrm{Suppose}\:\mathrm{the}\:\mathrm{inequality}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n}=\mathrm{k} \\ $$$$\mathrm{i}.\mathrm{e}\:\mathrm{5}^{\mathrm{k}} \geqslant\mathrm{1}+\mathrm{4k}.\mathrm{Then}\:\mathrm{5}^{\mathrm{k}+\mathrm{1}} =\mathrm{5}.\mathrm{5}^{\mathrm{k}} \geqslant\mathrm{5}\left(\mathrm{1}+\mathrm{4k}\right) \\ $$$$=\mathrm{5}+\mathrm{20k}\geqslant\mathrm{5}+\mathrm{4k}=\mathrm{1}+\mathrm{4}\left(\mathrm{k}+\mathrm{1}\right)\mathrm{which} \\ $$$$\mathrm{shows}\:\mathrm{the}\:\mathrm{inequality}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n}=\mathrm{k}+\mathrm{1} \\ $$$$\mathrm{By}\:\mathrm{induction}\:\mathrm{principle}\:\mathrm{the}\:\mathrm{inequality}\:\mathrm{is}\: \\ $$$$\mathrm{true}\:\mathrm{for}\:\forall\mathrm{n}\in\mathrm{N}\left(\mathrm{q}.\mathrm{e}.\mathrm{d}\right) \\ $$

Answered by Bird last updated on 21/Oct/20

n=0 we get 1≥1+0 (true) let suppose 5^n ≥1+4n and prove 5^(n+1) ≥1+4(n+1) we hsve 5^n ≥1+4n(hypothese) ⇒ 5^(n+1) ≥5(1+4n)=5+20n we have 5+20n−(1+4(n+1)) =5+20n−5−4n =16n≥0 ⇒ 5^(n+1) ≥1+4(n+1) so the relation is true at term n+1

$${n}=\mathrm{0}\:\:{we}\:{get}\:\mathrm{1}\geqslant\mathrm{1}+\mathrm{0}\:\left({true}\right) \\ $$$${let}\:{suppose}\:\mathrm{5}^{{n}} \geqslant\mathrm{1}+\mathrm{4}{n}\:{and}\:{prove} \\ $$$$\mathrm{5}^{{n}+\mathrm{1}} \geqslant\mathrm{1}+\mathrm{4}\left({n}+\mathrm{1}\right)\:\:{we}\:{hsve} \\ $$$$\mathrm{5}^{{n}} \geqslant\mathrm{1}+\mathrm{4}{n}\left({hypothese}\right)\:\Rightarrow \\ $$$$\mathrm{5}^{{n}+\mathrm{1}} \geqslant\mathrm{5}\left(\mathrm{1}+\mathrm{4}{n}\right)=\mathrm{5}+\mathrm{20}{n} \\ $$$${we}\:{have}\:\mathrm{5}+\mathrm{20}{n}−\left(\mathrm{1}+\mathrm{4}\left({n}+\mathrm{1}\right)\right) \\ $$$$=\mathrm{5}+\mathrm{20}{n}−\mathrm{5}−\mathrm{4}{n}\:=\mathrm{16}{n}\geqslant\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{5}^{{n}+\mathrm{1}} \geqslant\mathrm{1}+\mathrm{4}\left({n}+\mathrm{1}\right)\:{so}\:{the}\:{relation} \\ $$$${is}\:{true}\:{at}\:{term}\:{n}+\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com