
Question Number 26693 by Tinkutara last updated on 28/Dec/17
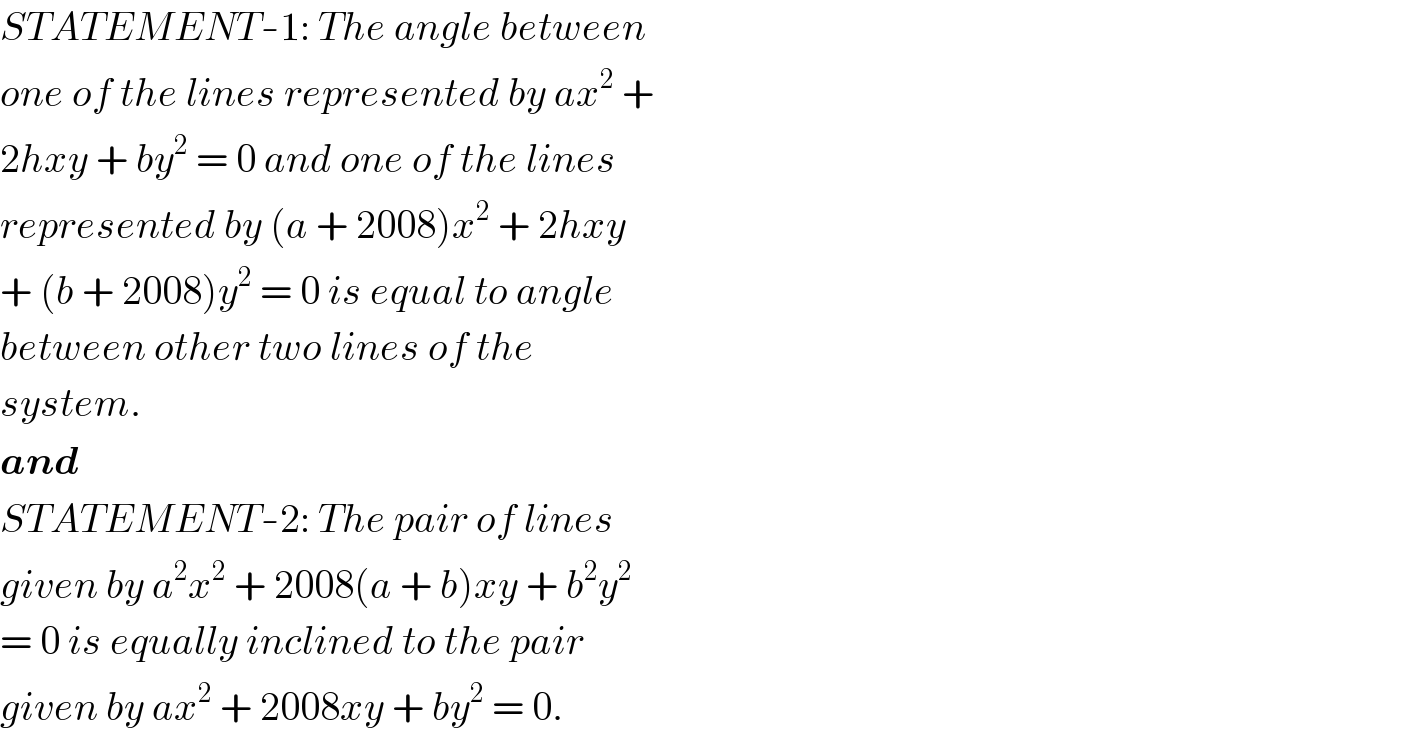
$${STATEMENT}-\mathrm{1}:\:{The}\:{angle}\:{between} \\ $$$${one}\:{of}\:{the}\:{lines}\:{represented}\:{by}\:{ax}^{\mathrm{2}} \:+ \\ $$$$\mathrm{2}{hxy}\:+\:{by}^{\mathrm{2}} \:=\:\mathrm{0}\:{and}\:{one}\:{of}\:{the}\:{lines} \\ $$$${represented}\:{by}\:\left({a}\:+\:\mathrm{2008}\right){x}^{\mathrm{2}} \:+\:\mathrm{2}{hxy} \\ $$$$+\:\left({b}\:+\:\mathrm{2008}\right){y}^{\mathrm{2}} \:=\:\mathrm{0}\:{is}\:{equal}\:{to}\:{angle} \\ $$$${between}\:{other}\:{two}\:{lines}\:{of}\:{the} \\ $$$${system}. \\ $$$$\boldsymbol{{and}} \\ $$$${STATEMENT}-\mathrm{2}:\:{The}\:{pair}\:{of}\:{lines} \\ $$$${given}\:{by}\:{a}^{\mathrm{2}} {x}^{\mathrm{2}} \:+\:\mathrm{2008}\left({a}\:+\:{b}\right){xy}\:+\:{b}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$$=\:\mathrm{0}\:{is}\:{equally}\:{inclined}\:{to}\:{the}\:{pair} \\ $$$${given}\:{by}\:{ax}^{\mathrm{2}} \:+\:\mathrm{2008}{xy}\:+\:{by}^{\mathrm{2}} \:=\:\mathrm{0}. \\ $$
Commented by Tinkutara last updated on 31/Dec/17
Anyone?
Commented by Tinkutara last updated on 31/Dec/17
Answer given is both true but Reason doesn't explain Assertion.
Commented by ajfour last updated on 31/Dec/17
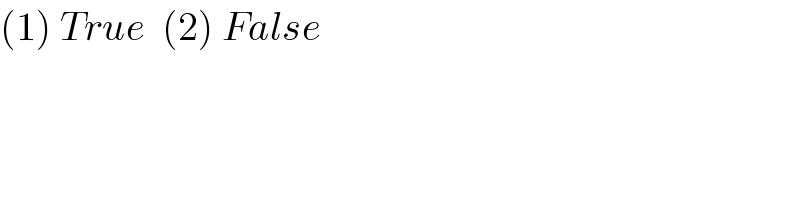
$$\left(\mathrm{1}\right)\:{True}\:\:\left(\mathrm{2}\right)\:{False} \\ $$
