
Question Number 190165 by TUN last updated on 29/Mar/23
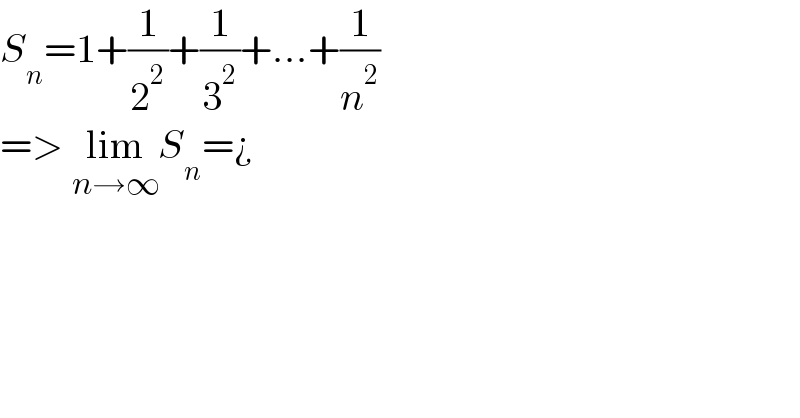
$${S}_{{n}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+...+\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$ $$=>\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{S}_{{n}} =¿ \\ $$
Answered by JDamian last updated on 29/Mar/23

$$\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$
Commented byTUN last updated on 10/Apr/23

$${how}\:{to}\:{solve}\:{it} \\ $$
