
Question Number 197906 by mnjuly1970 last updated on 03/Oct/23
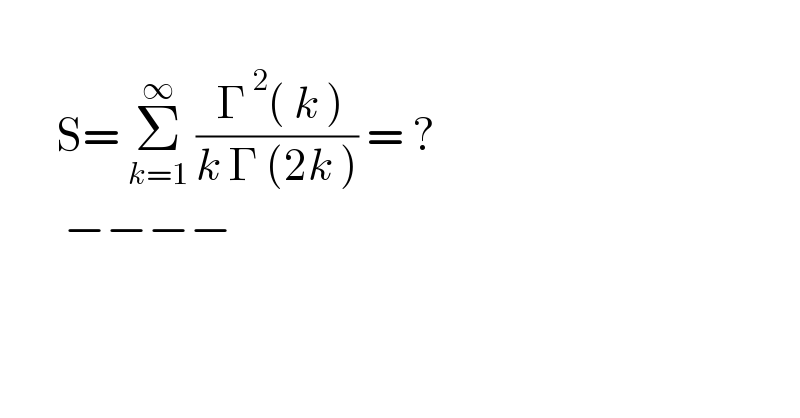
$$ \\ $$$$\:\:\:\:\:\:\:\mathrm{S}=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\:\Gamma^{\:\mathrm{2}} \left(\:{k}\:\right)}{{k}\:\Gamma\:\left(\mathrm{2}{k}\:\right)}\:=\:? \\ $$$$\:\:\:\:\:\:\:\:−−−− \\ $$
Answered by Dwan last updated on 03/Oct/23
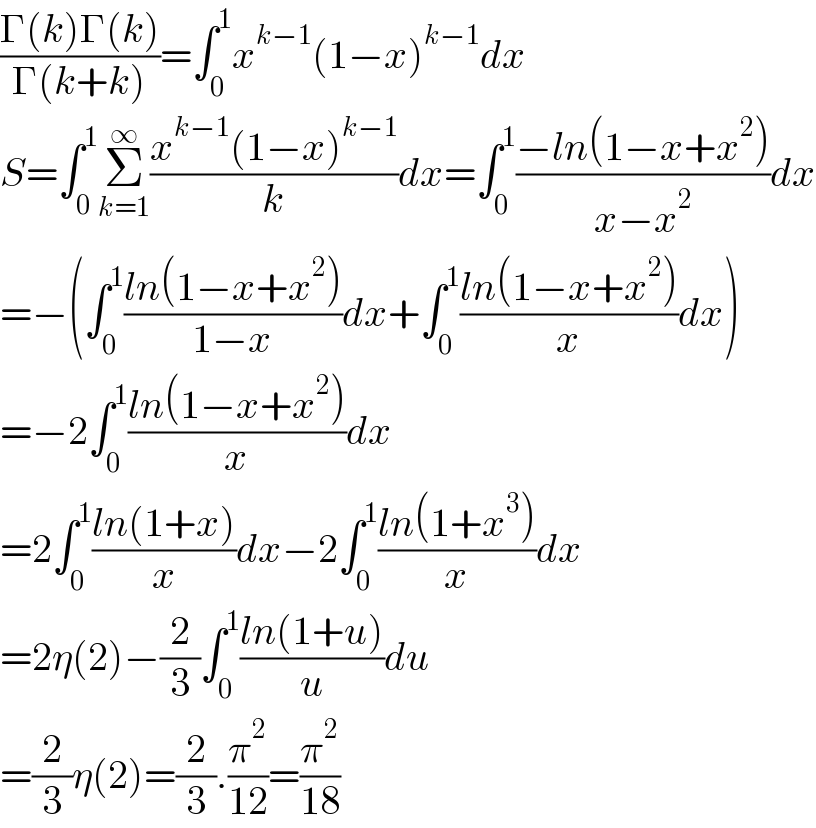
$$\frac{\Gamma\left({k}\right)\Gamma\left({k}\right)}{\Gamma\left({k}+{k}\right)}=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{k}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{k}−\mathrm{1}} {dx} \\ $$$${S}=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{k}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{k}−\mathrm{1}} }{{k}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−{ln}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)}{{x}−{x}^{\mathrm{2}} }{dx} \\ $$$$=−\left(\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)}{\mathrm{1}−{x}}{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)}{{x}}{dx}\right) \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)}{{x}}{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx}−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)}{{x}}{dx} \\ $$$$=\mathrm{2}\eta\left(\mathrm{2}\right)−\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{u}\right)}{{u}}{du} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\eta\left(\mathrm{2}\right)=\frac{\mathrm{2}}{\mathrm{3}}.\frac{\pi^{\mathrm{2}} }{\mathrm{12}}=\frac{\pi^{\mathrm{2}} }{\mathrm{18}} \\ $$
Commented by mnjuly1970 last updated on 04/Oct/23

$$\:\:\:\:{thanks}\:{alot}\:{sir}\: \\ $$$${so}\:{excellent}\:{solution}... \\ $$
