
Question Number 144068 by SOMEDAVONG last updated on 21/Jun/21
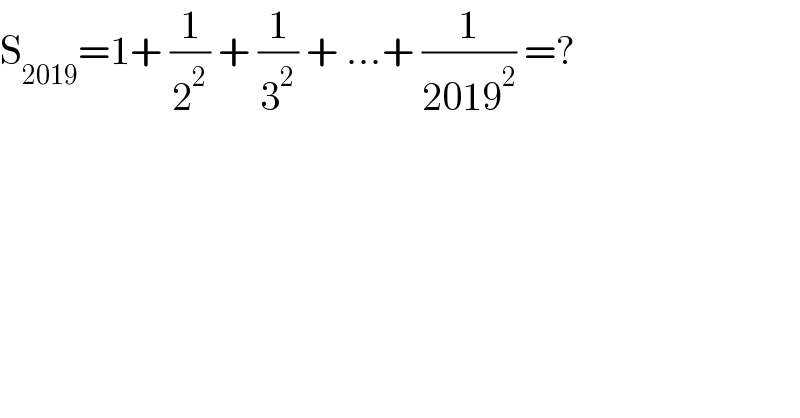
$$\mathrm{S}_{\mathrm{2019}} =\mathrm{1}+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }\:+\:...+\:\frac{\mathrm{1}}{\mathrm{2019}^{\mathrm{2}} }\:=? \\ $$
Answered by Olaf_Thorendsen last updated on 21/Jun/21
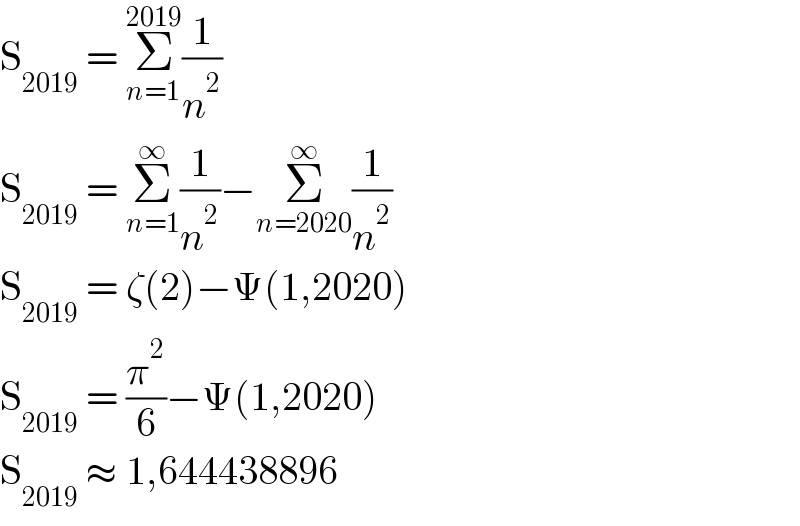
$$\mathrm{S}_{\mathrm{2019}} \:=\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{2019}} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$\mathrm{S}_{\mathrm{2019}} \:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\underset{{n}=\mathrm{2020}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$\mathrm{S}_{\mathrm{2019}} \:=\:\zeta\left(\mathrm{2}\right)−\Psi\left(\mathrm{1},\mathrm{2020}\right) \\ $$$$\mathrm{S}_{\mathrm{2019}} \:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\Psi\left(\mathrm{1},\mathrm{2020}\right) \\ $$$$\mathrm{S}_{\mathrm{2019}} \:\approx\:\mathrm{1},\mathrm{644438896} \\ $$
Commented by SOMEDAVONG last updated on 24/Jun/21

$$\mathrm{Thanks}\:\mathrm{sir}!! \\ $$
