Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Next in UNKNOWN      

Question Number 4882 by Rishabh Jain last updated on 19/Mar/16

Roots of the equation 9x^2 −18∣x∣+5=0 belonging to the domain of definition of the function f(x)=log (x^2 −x−2) is/ are

$$\mathrm{Roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{9}{x}^{\mathrm{2}} −\mathrm{18}\mid{x}\mid+\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{belonging}\:\mathrm{to}\:\mathrm{the}\:\mathrm{domain}\:\mathrm{of}\:\mathrm{definition} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{function}\:{f}\left({x}\right)=\mathrm{log}\:\left({x}^{\mathrm{2}} −{x}−\mathrm{2}\right)\:\mathrm{is}/ \\ $$$$\mathrm{are} \\ $$

Answered by Yozzii last updated on 19/Mar/16

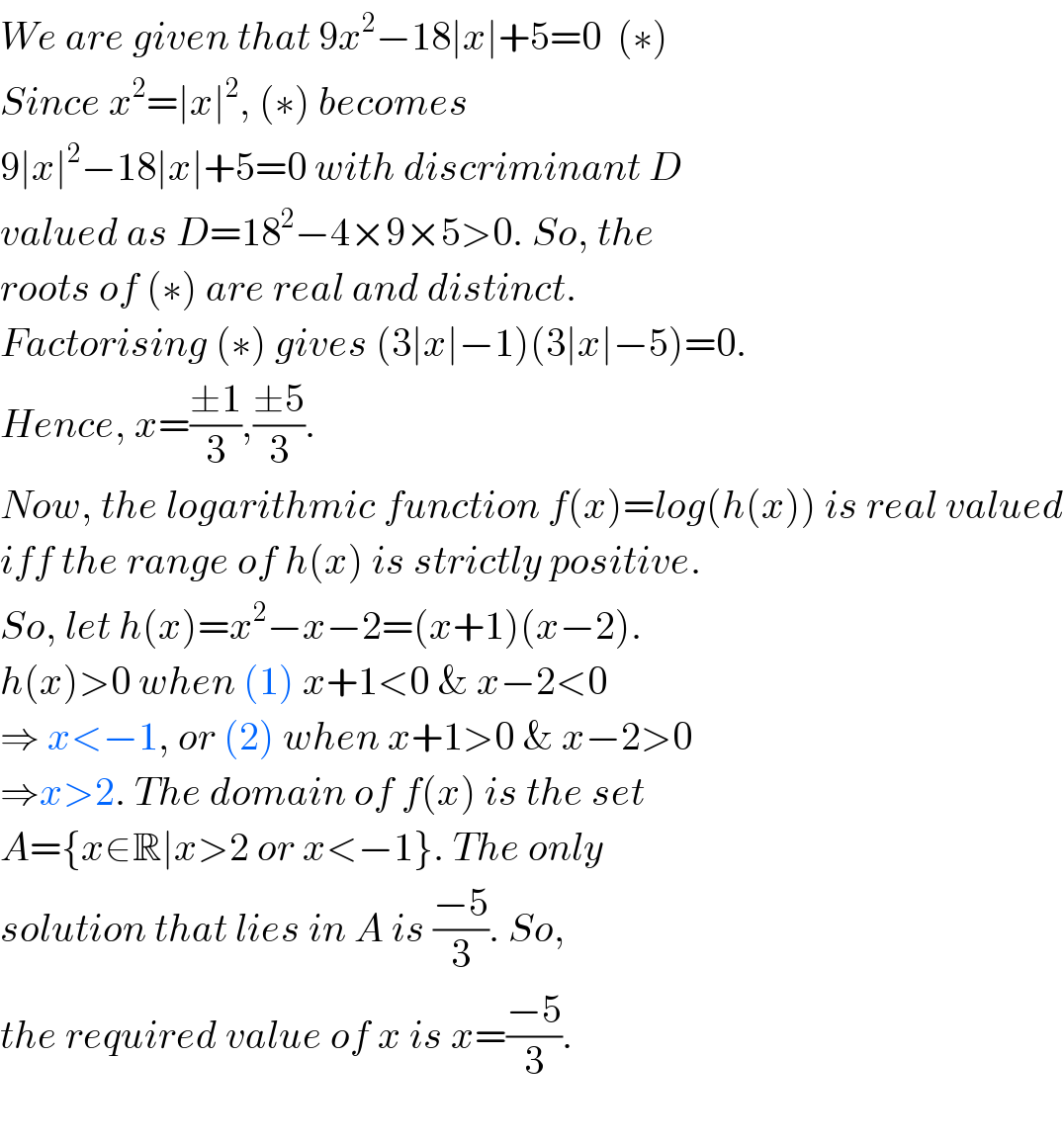
We are given that 9x^2 −18∣x∣+5=0 (∗) Since x^2 =∣x∣^2 , (∗) becomes 9∣x∣^2 −18∣x∣+5=0 with discriminant D valued as D=18^2 −4×9×5>0. So, the roots of (∗) are real and distinct. Factorising (∗) gives (3∣x∣−1)(3∣x∣−5)=0. Hence, x=((±1)/3),((±5)/3). Now, the logarithmic function f(x)=log(h(x)) is real valued iff the range of h(x) is strictly positive. So, let h(x)=x^2 −x−2=(x+1)(x−2). h(x)>0 when (1) x+1<0 & x−2<0 ⇒ x<−1, or (2) when x+1>0 & x−2>0 ⇒x>2. The domain of f(x) is the set A={x∈R∣x>2 or x<−1}. The only solution that lies in A is ((−5)/3). So, the required value of x is x=((−5)/3).

$${We}\:{are}\:{given}\:{that}\:\mathrm{9}{x}^{\mathrm{2}} −\mathrm{18}\mid{x}\mid+\mathrm{5}=\mathrm{0}\:\:\left(\ast\right) \\ $$$${Since}\:{x}^{\mathrm{2}} =\mid{x}\mid^{\mathrm{2}} ,\:\left(\ast\right)\:{becomes} \\ $$$$\mathrm{9}\mid{x}\mid^{\mathrm{2}} −\mathrm{18}\mid{x}\mid+\mathrm{5}=\mathrm{0}\:{with}\:{discriminant}\:{D} \\ $$$${valued}\:{as}\:{D}=\mathrm{18}^{\mathrm{2}} −\mathrm{4}×\mathrm{9}×\mathrm{5}>\mathrm{0}.\:{So},\:{the} \\ $$$${roots}\:{of}\:\left(\ast\right)\:{are}\:{real}\:{and}\:{distinct}.\: \\ $$$${Factorising}\:\left(\ast\right)\:{gives}\:\left(\mathrm{3}\mid{x}\mid−\mathrm{1}\right)\left(\mathrm{3}\mid{x}\mid−\mathrm{5}\right)=\mathrm{0}. \\ $$$${Hence},\:{x}=\frac{\pm\mathrm{1}}{\mathrm{3}},\frac{\pm\mathrm{5}}{\mathrm{3}}. \\ $$$${Now},\:{the}\:{logarithmic}\:{function}\:{f}\left({x}\right)={log}\left({h}\left({x}\right)\right)\:{is}\:{real}\:{valued} \\ $$$${iff}\:{the}\:{range}\:{of}\:{h}\left({x}\right)\:{is}\:{strictly}\:{positive}. \\ $$$${So},\:{let}\:{h}\left({x}\right)={x}^{\mathrm{2}} −{x}−\mathrm{2}=\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right). \\ $$$${h}\left({x}\right)>\mathrm{0}\:{when}\:\left(\mathrm{1}\right)\:{x}+\mathrm{1}<\mathrm{0}\:\&\:{x}−\mathrm{2}<\mathrm{0} \\ $$$$\Rightarrow\:{x}<−\mathrm{1},\:{or}\:\left(\mathrm{2}\right)\:{when}\:{x}+\mathrm{1}>\mathrm{0}\:\&\:{x}−\mathrm{2}>\mathrm{0} \\ $$$$\Rightarrow{x}>\mathrm{2}.\:{The}\:{domain}\:{of}\:{f}\left({x}\right)\:{is}\:{the}\:{set} \\ $$$${A}=\left\{{x}\in\mathbb{R}\mid{x}>\mathrm{2}\:{or}\:{x}<−\mathrm{1}\right\}.\:{The}\:{only}\: \\ $$$${solution}\:{that}\:{lies}\:{in}\:{A}\:{is}\:\frac{−\mathrm{5}}{\mathrm{3}}.\:{So}, \\ $$$${the}\:{required}\:{value}\:{of}\:{x}\:{is}\:{x}=\frac{−\mathrm{5}}{\mathrm{3}}. \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com