Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 159309 by LEKOUMA last updated on 15/Nov/21

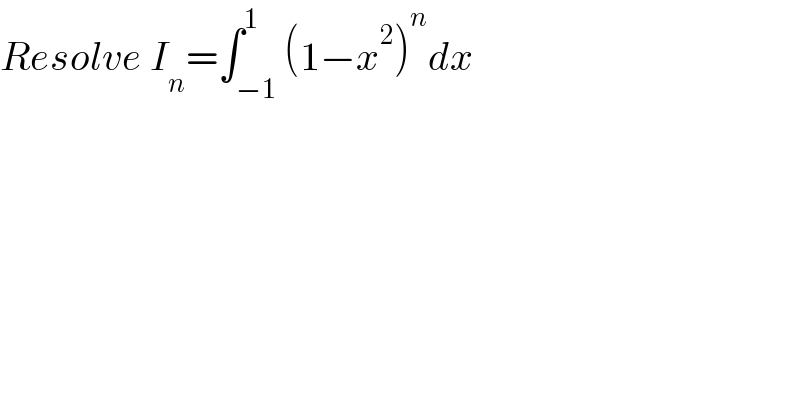
Resolve I_n =∫_(−1) ^1 (1−x^2 )^n dx

$${Resolve}\:{I}_{{n}} =\int_{−\mathrm{1}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}} {dx} \\ $$

Answered by mathmax by abdo last updated on 15/Nov/21

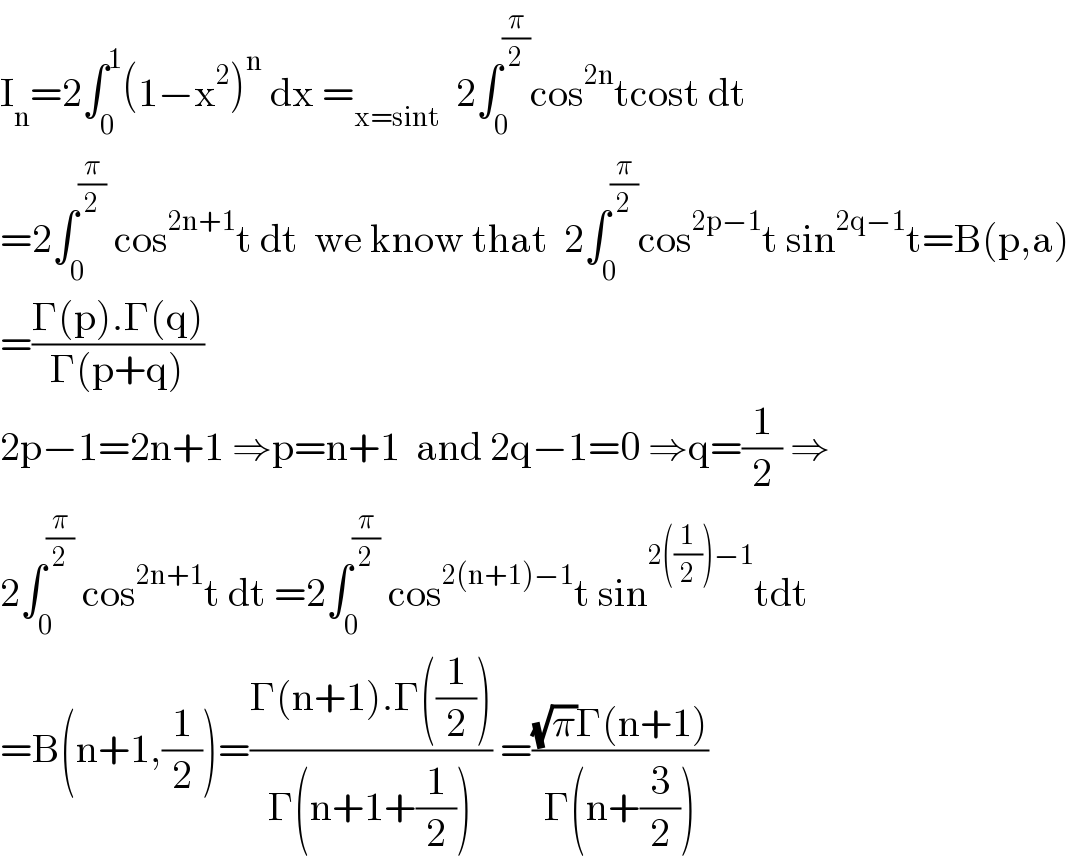
I_n =2∫_0 ^1 (1−x^2 )^n dx =_(x=sint) 2∫_0 ^(π/2) cos^(2n) tcost dt =2∫_0 ^(π/2) cos^(2n+1) t dt we know that 2∫_0 ^(π/2) cos^(2p−1) t sin^(2q−1) t=B(p,a) =((Γ(p).Γ(q))/(Γ(p+q))) 2p−1=2n+1 ⇒p=n+1 and 2q−1=0 ⇒q=(1/2) ⇒ 2∫_0 ^(π/2) cos^(2n+1) t dt =2∫_0 ^(π/2) cos^(2(n+1)−1) t sin^(2((1/2))−1) tdt =B(n+1,(1/2))=((Γ(n+1).Γ((1/2)))/(Γ(n+1+(1/2)))) =(((√π)Γ(n+1))/(Γ(n+(3/2))))

$$\mathrm{I}_{\mathrm{n}} =\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} \:\mathrm{dx}\:=_{\mathrm{x}=\mathrm{sint}} \:\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2n}} \mathrm{tcost}\:\mathrm{dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2n}+\mathrm{1}} \mathrm{t}\:\mathrm{dt}\:\:\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2p}−\mathrm{1}} \mathrm{t}\:\mathrm{sin}^{\mathrm{2q}−\mathrm{1}} \mathrm{t}=\mathrm{B}\left(\mathrm{p},\mathrm{a}\right) \\ $$$$=\frac{\Gamma\left(\mathrm{p}\right).\Gamma\left(\mathrm{q}\right)}{\Gamma\left(\mathrm{p}+\mathrm{q}\right)} \\ $$$$\mathrm{2p}−\mathrm{1}=\mathrm{2n}+\mathrm{1}\:\Rightarrow\mathrm{p}=\mathrm{n}+\mathrm{1}\:\:\mathrm{and}\:\mathrm{2q}−\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{q}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2n}+\mathrm{1}} \mathrm{t}\:\mathrm{dt}\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)−\mathrm{1}} \mathrm{t}\:\mathrm{sin}^{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{1}} \mathrm{tdt} \\ $$$$=\mathrm{B}\left(\mathrm{n}+\mathrm{1},\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\Gamma\left(\mathrm{n}+\mathrm{1}\right).\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{n}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\:=\frac{\sqrt{\pi}\Gamma\left(\mathrm{n}+\mathrm{1}\right)}{\Gamma\left(\mathrm{n}+\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com