Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 59626 by naka3546 last updated on 12/May/19

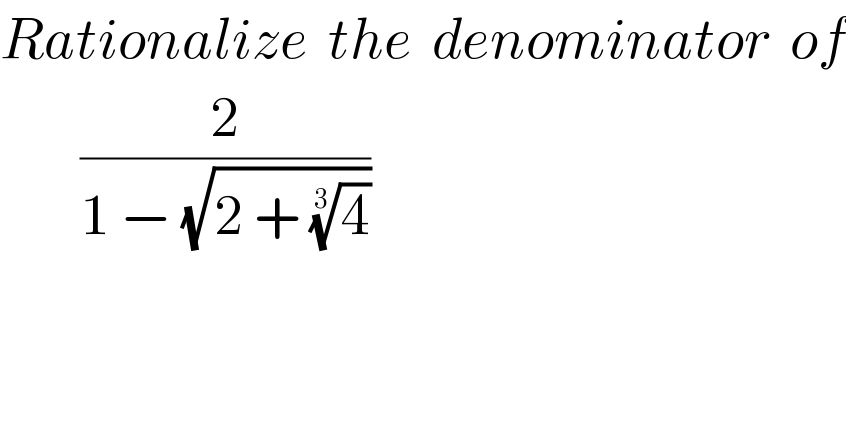
Rationalize the denominator of (2/(1 − (√(2 + (4)^(1/3) ))))

$${Rationalize}\:\:{the}\:\:{denominator}\:\:{of} \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{1}\:−\:\sqrt{\mathrm{2}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{4}}}} \\ $$

Answered by MJS last updated on 12/May/19

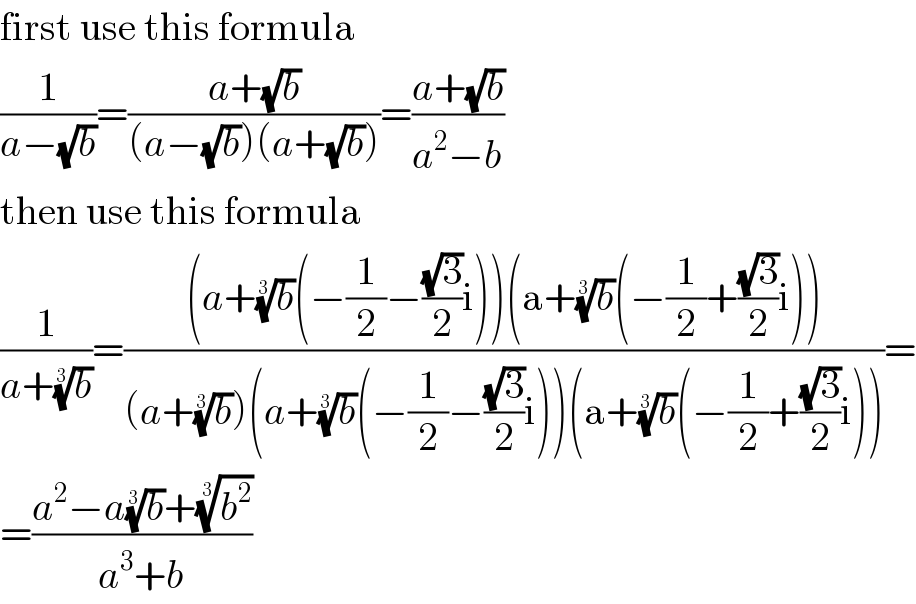
first use this formula (1/(a−(√b)))=((a+(√b))/((a−(√b))(a+(√b))))=((a+(√b))/(a^2 −b)) then use this formula (1/(a+(b)^(1/3) ))=(((a+(b)^(1/3) (−(1/2)−((√3)/2)i))(a+(b)^(1/3) (−(1/2)+((√3)/2)i)))/((a+(b)^(1/3) )(a+(b)^(1/3) (−(1/2)−((√3)/2)i))(a+(b)^(1/3) (−(1/2)+((√3)/2)i))))= =((a^2 −a(b)^(1/3) +(b^2 )^(1/3) )/(a^3 +b))

$$\mathrm{first}\:\mathrm{use}\:\mathrm{this}\:\mathrm{formula} \\ $$$$\frac{\mathrm{1}}{{a}−\sqrt{{b}}}=\frac{{a}+\sqrt{{b}}}{\left({a}−\sqrt{{b}}\right)\left({a}+\sqrt{{b}}\right)}=\frac{{a}+\sqrt{{b}}}{{a}^{\mathrm{2}} −{b}} \\ $$$$\mathrm{then}\:\mathrm{use}\:\mathrm{this}\:\mathrm{formula} \\ $$$$\frac{\mathrm{1}}{{a}+\sqrt[{\mathrm{3}}]{{b}}}=\frac{\left({a}+\sqrt[{\mathrm{3}}]{{b}}\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\right)\left(\mathrm{a}+\sqrt[{\mathrm{3}}]{{b}}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\right)}{\left({a}+\sqrt[{\mathrm{3}}]{{b}}\right)\left({a}+\sqrt[{\mathrm{3}}]{{b}}\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\right)\left(\mathrm{a}+\sqrt[{\mathrm{3}}]{{b}}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\right)}= \\ $$$$=\frac{{a}^{\mathrm{2}} −{a}\sqrt[{\mathrm{3}}]{{b}}+\sqrt[{\mathrm{3}}]{{b}^{\mathrm{2}} }}{{a}^{\mathrm{3}} +{b}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com