
Question Number 139404 by mnjuly1970 last updated on 26/Apr/21
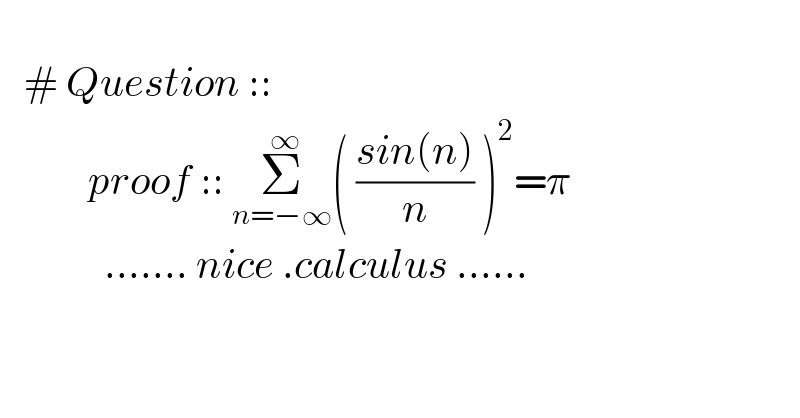
$$\:\:\:\:\: \\ $$$$\:\:\:#\:{Question}\::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{proof}\:::\:\underset{{n}=−\infty} {\overset{\:\infty} {\sum}}\left(\:\frac{{sin}\left({n}\right)}{{n}}\:\right)^{\mathrm{2}} =\pi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:.......\:{nice}\:.{calculus}\:......\:\:\:\:\: \\ $$
Answered by Dwaipayan Shikari last updated on 26/Apr/21
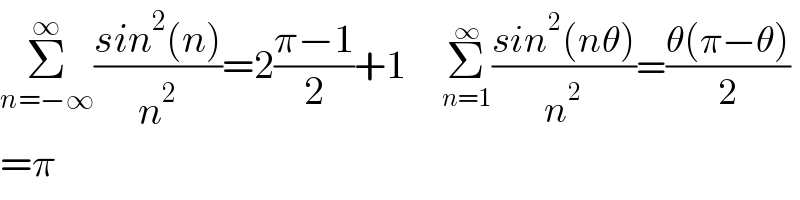
$$\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{{sin}^{\mathrm{2}} \left({n}\right)}{{n}^{\mathrm{2}} }=\mathrm{2}\frac{\pi−\mathrm{1}}{\mathrm{2}}+\mathrm{1}\:\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sin}^{\mathrm{2}} \left({n}\theta\right)}{{n}^{\mathrm{2}} }=\frac{\theta\left(\pi−\theta\right)}{\mathrm{2}} \\ $$$$=\pi \\ $$
Commented by mnjuly1970 last updated on 26/Apr/21

$${thanks}\:{alot}.. \\ $$
