
Question Number 192142 by mehdee42 last updated on 09/May/23
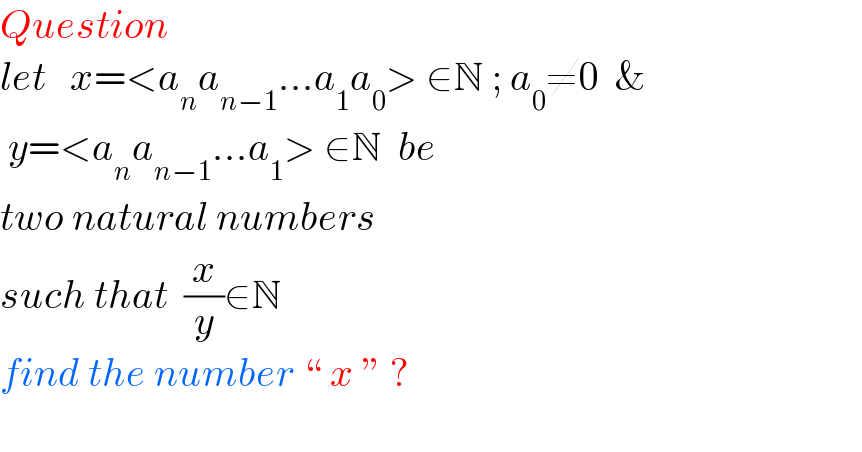
$${Question} \\ $$$${let}\:\:\:{x}=<{a}_{{n}} {a}_{{n}−\mathrm{1}} ...{a}_{\mathrm{1}} {a}_{\mathrm{0}} >\:\in\mathbb{N}\:;\:{a}_{\mathrm{0}} \neq\mathrm{0}\:\:\&\: \\ $$$$\:{y}=<{a}_{{n}} {a}_{{n}−\mathrm{1}} ...{a}_{\mathrm{1}} >\:\in\mathbb{N}\:\:{be}\: \\ $$$${two}\:{natural}\:{numbers}\: \\ $$$${such}\:{that}\:\:\frac{{x}}{{y}}\in\mathbb{N}\: \\ $$$${find}\:{the}\:{number}\:``\:{x}\:''\:? \\ $$$$ \\ $$
Answered by deleteduser1 last updated on 09/May/23

$${For}\:{a}\:\mathrm{2}-{digit}\:{number},{x};{possible}\:{values}: \\ $$$$\mathrm{99},\mathrm{88},\mathrm{77},\mathrm{66},\mathrm{55},\mathrm{48},\mathrm{44},\mathrm{39},\mathrm{36},\mathrm{33},\mathrm{28},\mathrm{26},...,\mathrm{22},\mathrm{19},...,\mathrm{11} \\ $$$$ \\ $$$${Now},{for}\:{an}\:{n}-{digit}\:{number}\left({n}\:{atleast}\:\mathrm{3}\right) \\ $$$$\left({where}\:{a}_{\mathrm{0}} \neq\mathrm{0}\right) \\ $$$$\frac{{x}}{{y}}=\frac{\mathrm{10}{x}}{{x}−{a}_{\mathrm{0}} }=\frac{\mathrm{10}\left({x}−{a}_{\mathrm{0}} \right)+\mathrm{10}{a}_{\mathrm{0}} }{{x}−{a}_{\mathrm{0}} }=\mathrm{10}+\frac{\mathrm{10}{a}_{\mathrm{0}} }{{x}−{a}_{\mathrm{0}} } \\ $$$$\Rightarrow{x}−{a}_{\mathrm{0}} \mid\mathrm{10}{a}_{\mathrm{0}} \Rightarrow{x}−{a}_{\mathrm{0}} \leqslant\mathrm{10}{a}_{\mathrm{0}} \\ $$$$\Rightarrow\mathrm{11}{a}_{\mathrm{0}} \geqslant{x} \\ $$$${But}\:{this}\:{is}\:{impossible}\:{since}\:{max}\left\{\mathrm{11}{a}_{\mathrm{0}} \right\}=\mathrm{99} \\ $$$${which}\:{is}\:{not}\:{atleast}\:{a}\:\mathrm{3}-{digit}\:{number}. \\ $$$$\Rightarrow{Only}\:\mathrm{2}-{digit}\:{solutions}\:{exist}. \\ $$
Commented by mehdee42 last updated on 09/May/23

$${it}\:{is}\:{very}\:{beautiful}\:{solution}. \\ $$$${in}\:{addition}\:{according}\:{to}\:{the}\:{condition}\:``\:{a}_{\mathrm{0}} \neq\mathrm{0}'' \\ $$$${x}\neq\mathrm{10},\mathrm{20},...,\mathrm{90} \\ $$
