Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 13733 by prakash jain last updated on 22/May/17

Question continuing from mrW1 post on p^2 mod n≡1. Find a number n such that for all m<n such that HCF(m,n)=1 m^2 mod n =1 e.g. for 12 possible value of m are 1,5,7,11.

$$\mathrm{Question}\:\mathrm{continuing}\:\mathrm{from} \\ $$$$\mathrm{mrW1}\:\mathrm{post}\:\mathrm{on}\:{p}^{\mathrm{2}} \:\mathrm{mod}\:\mathrm{n}\equiv\mathrm{1}. \\ $$$$\mathrm{Find}\:\mathrm{a}\:\mathrm{number}\:{n}\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{for}\:\mathrm{all}\:{m}<{n}\:\mathrm{such}\:\mathrm{that}\:\mathrm{HCF}\left({m},{n}\right)=\mathrm{1} \\ $$$${m}^{\mathrm{2}} \:\mathrm{mod}\:{n}\:=\mathrm{1} \\ $$$${e}.{g}.\:\mathrm{for}\:\mathrm{12}\:\mathrm{possible}\:\mathrm{value}\:\mathrm{of}\:{m} \\ $$$$\mathrm{are}\:\mathrm{1},\mathrm{5},\mathrm{7},\mathrm{11}. \\ $$

Commented by prakash jain last updated on 22/May/17

This will be sufficient condition for p^2 mod n=1. Can be considered necessary if we assume that for m<n where HCF(m,n)=1 there exists at least one prime of the form ln+m where (l,m,n) are natural numbers.

$$\mathrm{This}\:\mathrm{will}\:\mathrm{be}\:\mathrm{sufficient}\:\mathrm{condition} \\ $$$$\mathrm{for}\:{p}^{\mathrm{2}} \:\mathrm{mod}\:{n}=\mathrm{1}. \\ $$$$\mathrm{Can}\:\mathrm{be}\:\mathrm{considered}\:\mathrm{necessary}\:\mathrm{if}\:\mathrm{we} \\ $$$$\mathrm{assume}\:\mathrm{that}\:\mathrm{for}\:{m}<{n}\:\mathrm{where} \\ $$$$\mathrm{HCF}\left({m},{n}\right)=\mathrm{1}\:\mathrm{there}\:\mathrm{exists}\:\mathrm{at} \\ $$$$\mathrm{least}\:\mathrm{one}\:\mathrm{prime}\:\mathrm{of}\:\mathrm{the}\:\mathrm{form} \\ $$$${ln}+{m}\:\:\mathrm{where}\:\left({l},{m},{n}\right)\:\mathrm{are}\:\mathrm{natural}\:\mathrm{numbers}. \\ $$

Commented by mrW1 last updated on 23/May/17

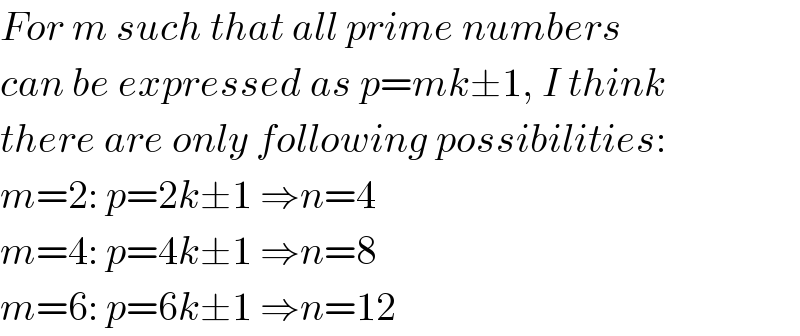
For m such that all prime numbers can be expressed as p=mk±1, I think there are only following possibilities: m=2: p=2k±1 ⇒n=4 m=4: p=4k±1 ⇒n=8 m=6: p=6k±1 ⇒n=12

$${For}\:{m}\:{such}\:{that}\:{all}\:{prime}\:{numbers} \\ $$$${can}\:{be}\:{expressed}\:{as}\:{p}={mk}\pm\mathrm{1},\:{I}\:{think} \\ $$$${there}\:{are}\:{only}\:{following}\:{possibilities}: \\ $$$${m}=\mathrm{2}:\:{p}=\mathrm{2}{k}\pm\mathrm{1}\:\Rightarrow{n}=\mathrm{4} \\ $$$${m}=\mathrm{4}:\:{p}=\mathrm{4}{k}\pm\mathrm{1}\:\Rightarrow{n}=\mathrm{8} \\ $$$${m}=\mathrm{6}:\:{p}=\mathrm{6}{k}\pm\mathrm{1}\:\Rightarrow{n}=\mathrm{12} \\ $$

Commented by prakash jain last updated on 23/May/17

Yes. For any number n we can express all primes as mn+k where HCF(k,n)=1,k<n (mn+k)^2 mod n=k^2 mod n n=12⇒k=1,5,7,11 5^2 ≡1 (mod 12) 7^2 ≡1 (mod 12) Now the question is to find n where k^2 mod n=1 (HCF(k,n)=1,k<n) (or to prove that no such n exist).

$$\mathrm{Yes}.\:\mathrm{For}\:\mathrm{any}\:\mathrm{number}\:{n}\:\mathrm{we}\:\mathrm{can}\: \\ $$$$\mathrm{express}\:\mathrm{all}\:\mathrm{primes}\:\mathrm{as} \\ $$$${mn}+{k}\:\mathrm{where}\:\mathrm{HCF}\left({k},{n}\right)=\mathrm{1},{k}<{n} \\ $$$$\left({mn}+{k}\right)^{\mathrm{2}} \:\mathrm{mod}\:\mathrm{n}={k}^{\mathrm{2}} \:\mathrm{mod}\:{n} \\ $$$${n}=\mathrm{12}\Rightarrow{k}=\mathrm{1},\mathrm{5},\mathrm{7},\mathrm{11} \\ $$$$\mathrm{5}^{\mathrm{2}} \equiv\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{12}\right) \\ $$$$\mathrm{7}^{\mathrm{2}} \equiv\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{12}\right)\: \\ $$$$\mathrm{Now}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{to}\:\mathrm{find}\:{n}\:\mathrm{where} \\ $$$${k}^{\mathrm{2}} \:\mathrm{mod}\:{n}=\mathrm{1}\:\left(\mathrm{HCF}\left({k},{n}\right)=\mathrm{1},{k}<{n}\right) \\ $$$$\left(\mathrm{or}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{no}\:\mathrm{such}\:{n}\:\mathrm{exist}\right). \\ $$

Commented by prakash jain last updated on 23/May/17

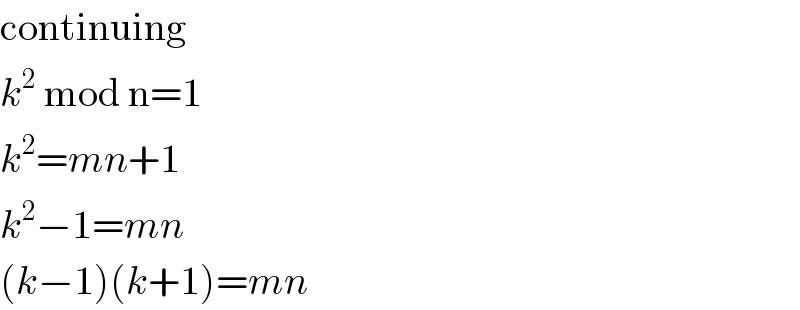
continuing k^2 mod n=1 k^2 =mn+1 k^2 −1=mn (k−1)(k+1)=mn

$$\mathrm{continuing} \\ $$$${k}^{\mathrm{2}} \:\mathrm{mod}\:\mathrm{n}=\mathrm{1} \\ $$$${k}^{\mathrm{2}} ={mn}+\mathrm{1} \\ $$$${k}^{\mathrm{2}} −\mathrm{1}={mn} \\ $$$$\left({k}−\mathrm{1}\right)\left({k}+\mathrm{1}\right)={mn} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com