
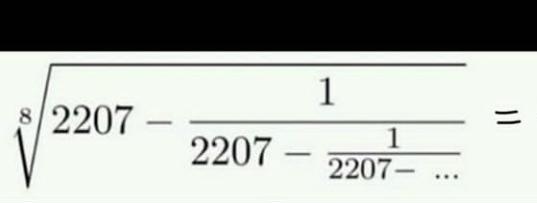
Question Number 99025 by joki last updated on 18/Jun/20
Commented by bobhans last updated on 18/Jun/20
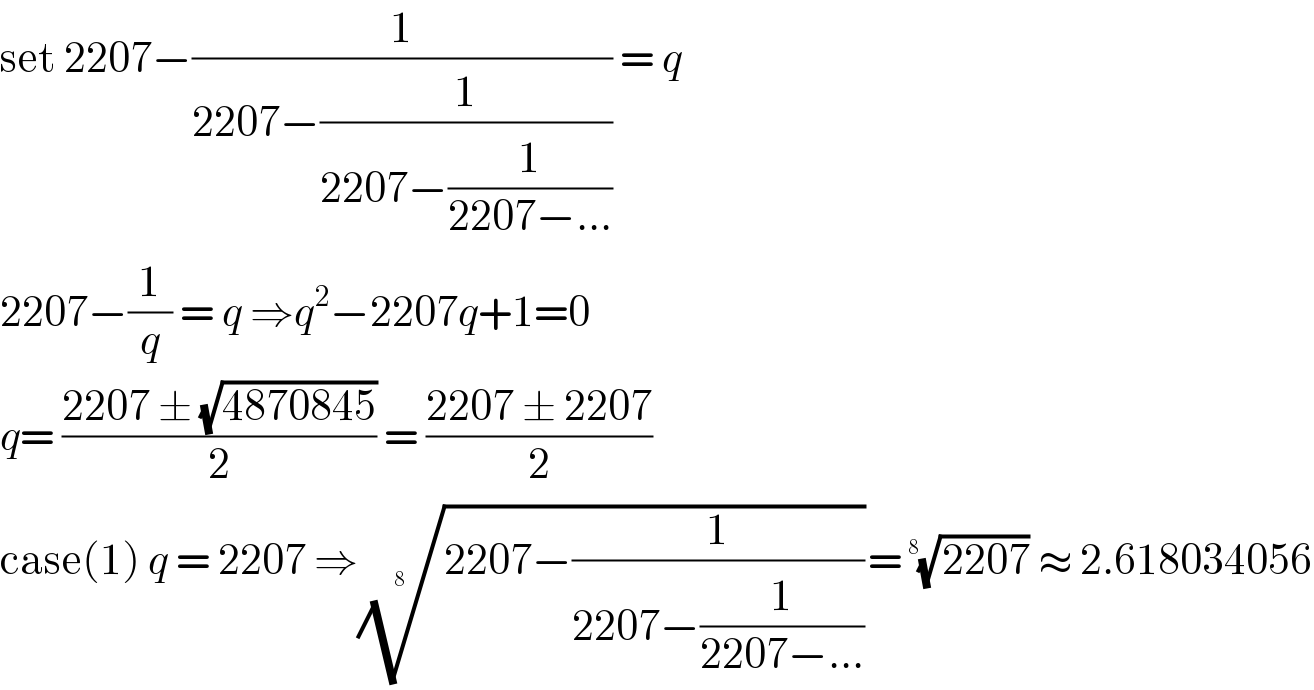
$$\mathrm{set}\:\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−...}}}\:=\:{q} \\ $$$$\mathrm{2207}−\frac{\mathrm{1}}{{q}}\:=\:{q}\:\Rightarrow{q}^{\mathrm{2}} −\mathrm{2207}{q}+\mathrm{1}=\mathrm{0} \\ $$$${q}=\:\frac{\mathrm{2207}\:\pm\:\sqrt{\mathrm{4870845}}}{\mathrm{2}}\:=\:\frac{\mathrm{2207}\:\pm\:\mathrm{2207}}{\mathrm{2}} \\ $$$$\mathrm{case}\left(\mathrm{1}\right)\:{q}\:=\:\mathrm{2207}\:\Rightarrow\sqrt[{\mathrm{8}\:\:}]{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−...}}}=\:\sqrt[{\mathrm{8}\:\:\:}]{\mathrm{2207}}\:\approx\:\mathrm{2}.\mathrm{618034056} \\ $$
Commented by joki last updated on 18/Jun/20

$${thanks}\:{sir} \\ $$
Commented by MJS last updated on 18/Jun/20
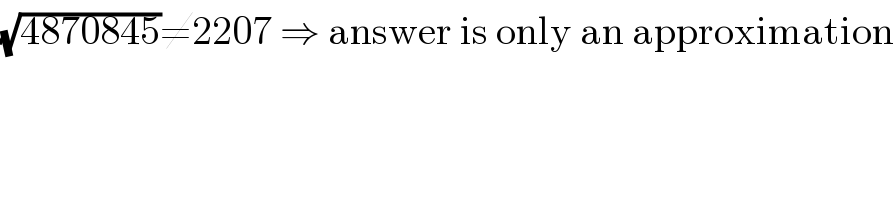
$$\sqrt{\mathrm{4870845}}\neq\mathrm{2207}\:\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{only}\:\mathrm{an}\:\mathrm{approximation} \\ $$
Commented by bobhans last updated on 18/Jun/20

$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{my}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{approximation} \\ $$
Answered by bemath last updated on 18/Jun/20
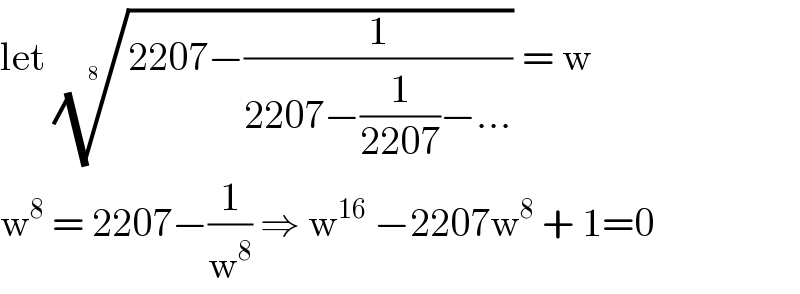
$$\mathrm{let}\:\sqrt[{\mathrm{8}\:\:}]{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}}−...}}\:=\:\mathrm{w} \\ $$$$\mathrm{w}^{\mathrm{8}} \:=\:\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{w}^{\mathrm{8}} }\:\Rightarrow\:\mathrm{w}^{\mathrm{16}} \:−\mathrm{2207w}^{\mathrm{8}} \:+\:\mathrm{1}=\mathrm{0} \\ $$
Commented by mr W last updated on 18/Jun/20

$${wrong}\:{sir}! \\ $$$${should}\:{be} \\ $$$$\mathrm{w}^{\mathrm{8}} \:=\:\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{w}^{\mathrm{8}} } \\ $$
Commented by joki last updated on 18/Jun/20
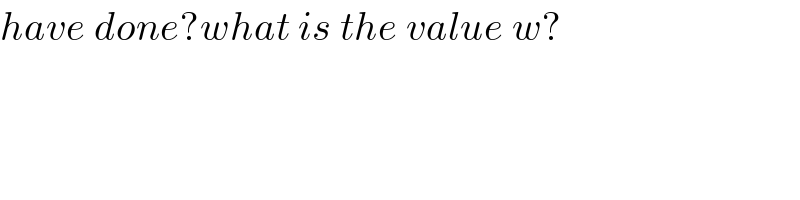
$${have}\:{done}?{what}\:{is}\:{the}\:{value}\:{w}? \\ $$
Commented by Rasheed.Sindhi last updated on 18/Jun/20
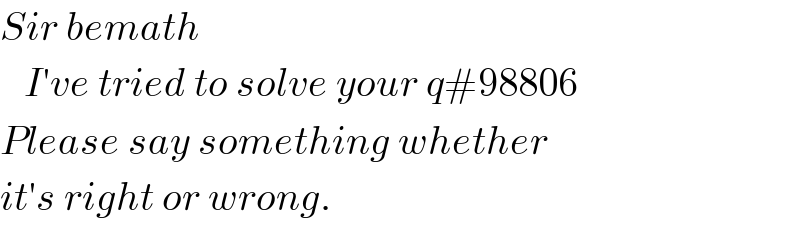
$${Sir}\:{bemath} \\ $$$$\:\:\:{I}'{ve}\:{tried}\:{to}\:{solve}\:{your}\:{q}#\mathrm{98806} \\ $$$${Please}\:{say}\:{something}\:{whether} \\ $$$${it}'{s}\:{right}\:{or}\:{wrong}. \\ $$
Commented by bemath last updated on 18/Jun/20
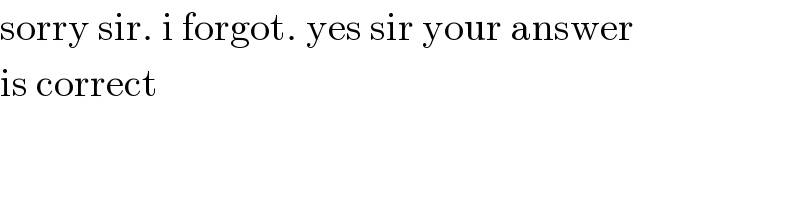
$$\mathrm{sorry}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{forgot}.\:\mathrm{yes}\:\mathrm{sir}\:\mathrm{your}\:\mathrm{answer}\: \\ $$$$\mathrm{is}\:\mathrm{correct} \\ $$
Commented by Rasheed.Sindhi last updated on 18/Jun/20

$${Thanx}\:{sir}! \\ $$
Answered by MJS last updated on 18/Jun/20

$${x}=\mathrm{2207}−\frac{\mathrm{1}}{{x}} \\ $$$${x}^{\mathrm{2}} −\mathrm{2207}{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{2207}\pm\mathrm{987}\sqrt{\mathrm{5}}}{\mathrm{2}};\:{x}\approx\mathrm{2207}\:\Rightarrow\:{x}=\frac{\mathrm{2207}+\mathrm{987}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\sqrt[{\mathrm{8}}]{{x}}=\sqrt{\sqrt{\sqrt{{x}}}} \\ $$$$\sqrt{\frac{\mathrm{2207}+\mathrm{987}\sqrt{\mathrm{5}}}{\mathrm{2}}}=\frac{\mathrm{47}+\mathrm{21}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\sqrt{\frac{\mathrm{47}+\mathrm{21}\sqrt{\mathrm{5}}}{\mathrm{2}}}=\frac{\mathrm{7}+\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\sqrt{\frac{\mathrm{7}+\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}}}=\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by mr W last updated on 18/Jun/20
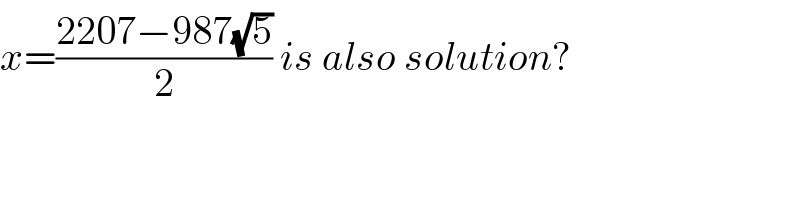
$${x}=\frac{\mathrm{2207}−\mathrm{987}\sqrt{\mathrm{5}}}{\mathrm{2}}\:{is}\:{also}\:{solution}? \\ $$
Commented by MJS last updated on 18/Jun/20
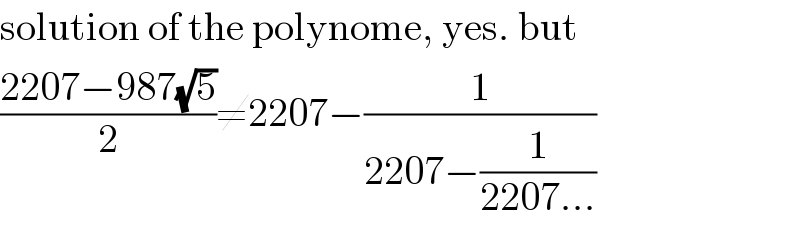
$$\mathrm{solution}\:\mathrm{of}\:\mathrm{the}\:\mathrm{polynome},\:\mathrm{yes}.\:\mathrm{but} \\ $$$$\frac{\mathrm{2207}−\mathrm{987}\sqrt{\mathrm{5}}}{\mathrm{2}}\neq\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}−\frac{\mathrm{1}}{\mathrm{2207}...}} \\ $$
Commented by bobhans last updated on 18/Jun/20

$$\mathrm{great}\:\mathrm{sir}... \\ $$
