
Question Number 9880 by sandipkd@ last updated on 12/Jan/17
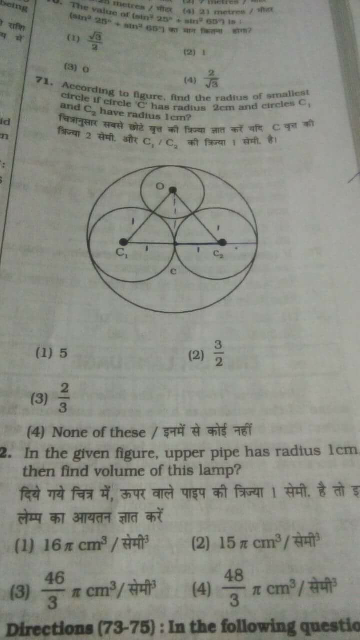
Answered by bansal22luvi@gmail.com last updated on 12/Jan/17
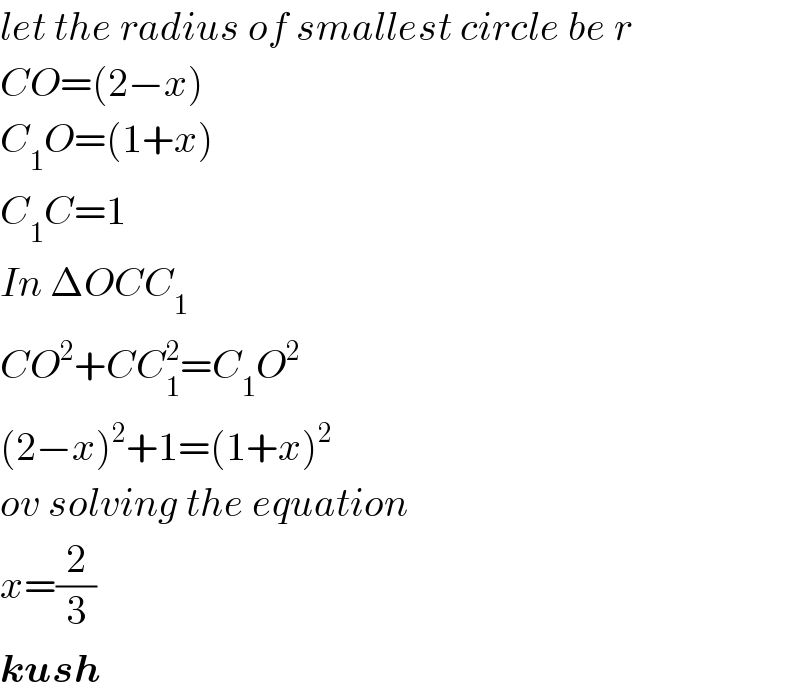
$${let}\:{the}\:{radius}\:{of}\:{smallest}\:{circle}\:{be}\:{r} \\ $$$${CO}=\left(\mathrm{2}−{x}\right) \\ $$$${C}_{\mathrm{1}} {O}=\left(\mathrm{1}+{x}\right) \\ $$$${C}_{\mathrm{1}} {C}=\mathrm{1} \\ $$$${In}\:\Delta{OCC}_{\mathrm{1}} \\ $$$${CO}^{\mathrm{2}} +{CC}_{\mathrm{1}} ^{\mathrm{2}} ={C}_{\mathrm{1}} {O}^{\mathrm{2}} \\ $$$$\left(\mathrm{2}−{x}\right)^{\mathrm{2}} +\mathrm{1}=\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \\ $$$${ov}\:{solving}\:{the}\:{equation} \\ $$$${x}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\boldsymbol{{kush}} \\ $$
Answered by mrW1 last updated on 12/Jan/17
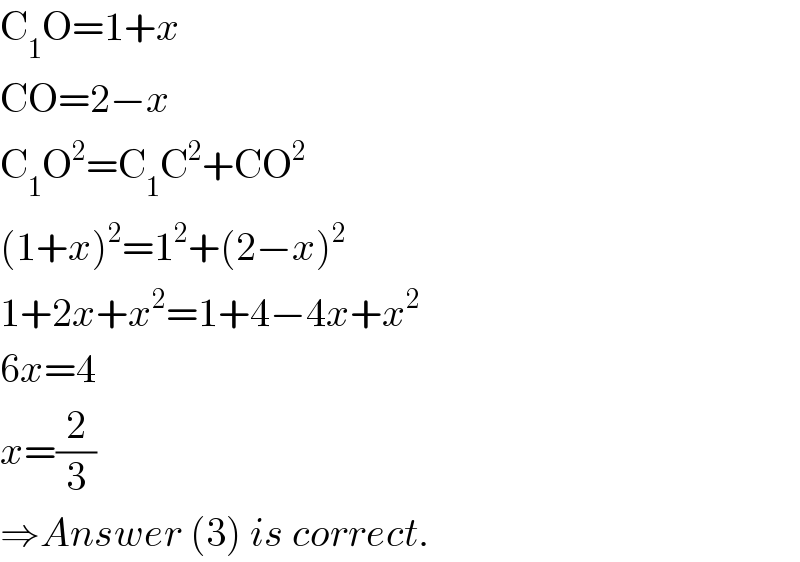
$$\mathrm{C}_{\mathrm{1}} \mathrm{O}=\mathrm{1}+{x} \\ $$$$\mathrm{CO}=\mathrm{2}−{x} \\ $$$$\mathrm{C}_{\mathrm{1}} \mathrm{O}^{\mathrm{2}} =\mathrm{C}_{\mathrm{1}} \mathrm{C}^{\mathrm{2}} +\mathrm{CO}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+{x}\right)^{\mathrm{2}} =\mathrm{1}^{\mathrm{2}} +\left(\mathrm{2}−{x}\right)^{\mathrm{2}} \\ $$$$\mathrm{1}+\mathrm{2}{x}+{x}^{\mathrm{2}} =\mathrm{1}+\mathrm{4}−\mathrm{4}{x}+{x}^{\mathrm{2}} \\ $$$$\mathrm{6}{x}=\mathrm{4} \\ $$$${x}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow{Answer}\:\left(\mathrm{3}\right)\:{is}\:{correct}. \\ $$
