
Question Number 98618 by Ar Brandon last updated on 15/Jun/20
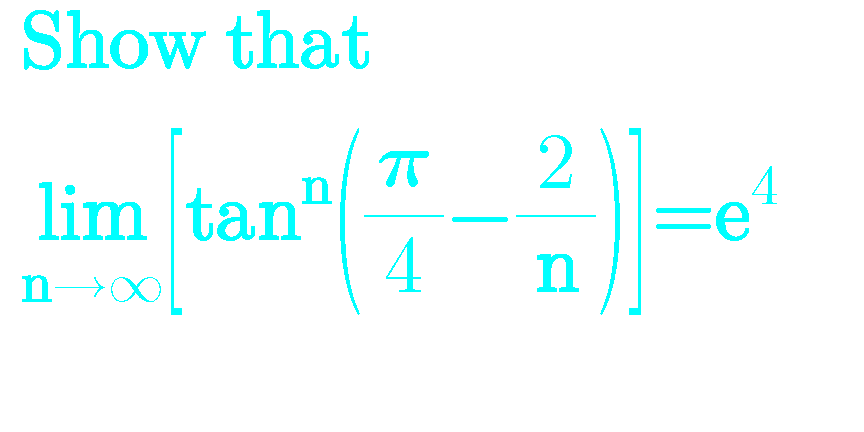
Answered by Ar Brandon last updated on 15/Jun/20

Commented by mr W last updated on 15/Jun/20
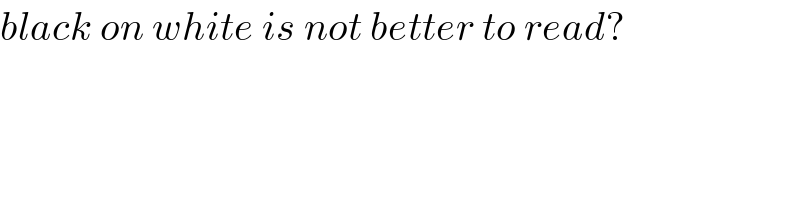
$${black}\:{on}\:{white}\:{is}\:{not}\:{better}\:{to}\:{read}? \\ $$
Commented by Ar Brandon last updated on 15/Jun/20
OK, understood. Just wanted to try something new.
Answered by maths mind last updated on 15/Jun/20
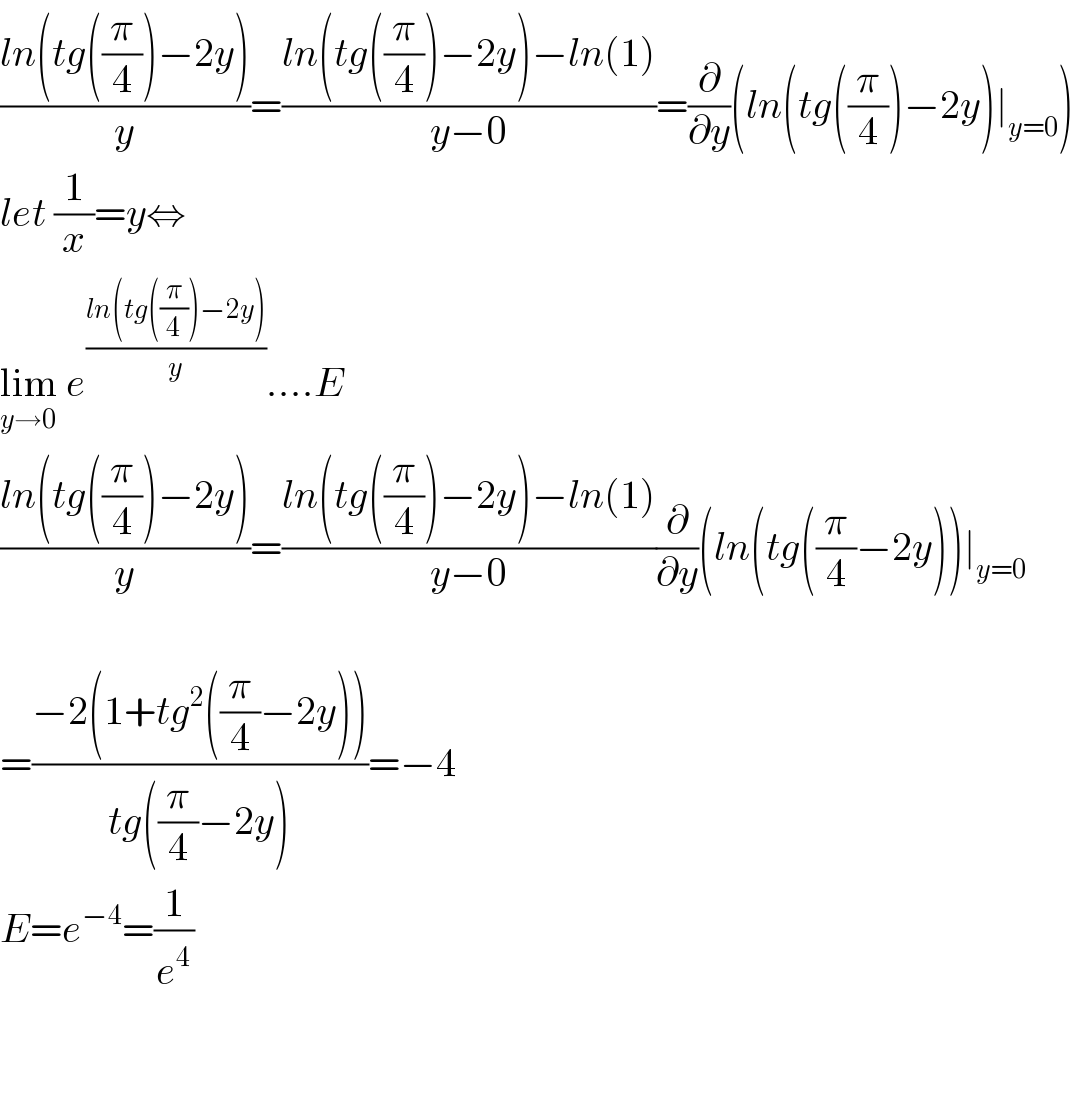
$$\frac{{ln}\left({tg}\left(\frac{\pi}{\mathrm{4}}\right)−\mathrm{2}{y}\right)}{{y}}=\frac{{ln}\left({tg}\left(\frac{\pi}{\mathrm{4}}\right)−\mathrm{2}{y}\right)−{ln}\left(\mathrm{1}\right)}{{y}−\mathrm{0}}=\frac{\partial}{\partial{y}}\left({ln}\left({tg}\left(\frac{\pi}{\mathrm{4}}\right)−\mathrm{2}{y}\right)\mid_{{y}=\mathrm{0}} \right) \\ $$$${let}\:\frac{\mathrm{1}}{{x}}={y}\Leftrightarrow \\ $$$$\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{e}^{\frac{{ln}\left({tg}\left(\frac{\pi}{\mathrm{4}}\right)−\mathrm{2}{y}\right)}{{y}}} ....{E} \\ $$$$\frac{{ln}\left({tg}\left(\frac{\pi}{\mathrm{4}}\right)−\mathrm{2}{y}\right)}{{y}}=\frac{{ln}\left({tg}\left(\frac{\pi}{\mathrm{4}}\right)−\mathrm{2}{y}\right)−{ln}\left(\mathrm{1}\right)}{{y}−\mathrm{0}}\frac{\partial}{\partial{y}}\left({ln}\left({tg}\left(\frac{\pi}{\mathrm{4}}−\mathrm{2}{y}\right)\right)\mid_{{y}=\mathrm{0}} \right. \\ $$$$ \\ $$$$=\frac{−\mathrm{2}\left(\mathrm{1}+{tg}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−\mathrm{2}{y}\right)\right)}{{tg}\left(\frac{\pi}{\mathrm{4}}−\mathrm{2}{y}\right)}=−\mathrm{4} \\ $$$${E}={e}^{−\mathrm{4}} =\frac{\mathrm{1}}{{e}^{\mathrm{4}} } \\ $$$$ \\ $$$$ \\ $$
