
Question Number 95604 by 174 last updated on 26/May/20
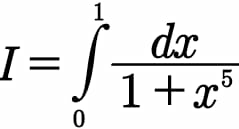
Commented by MJS last updated on 26/May/20
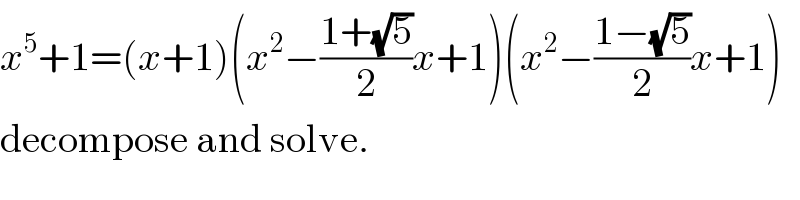
$${x}^{\mathrm{5}} +\mathrm{1}=\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}{x}+\mathrm{1}\right) \\ $$$$\mathrm{decompose}\:\mathrm{and}\:\mathrm{solve}. \\ $$
Commented by peter frank last updated on 26/May/20

$$\mathrm{sir}\:\mathrm{can}\:\mathrm{show}\:\mathrm{how}\:\mathrm{to}\:\mathrm{partialize} \\ $$$$\mathrm{given}\:\mathrm{equation}\:\mathrm{of}\: \\ $$$$\mathrm{decomposition}. \\ $$
Commented by Tony Lin last updated on 26/May/20
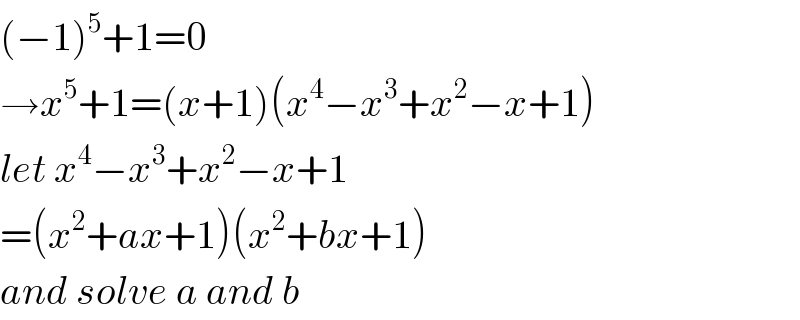
$$\left(−\mathrm{1}\right)^{\mathrm{5}} +\mathrm{1}=\mathrm{0} \\ $$$$\rightarrow{x}^{\mathrm{5}} +\mathrm{1}=\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −{x}+\mathrm{1}\right) \\ $$$${let}\:{x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$$=\left({x}^{\mathrm{2}} +{ax}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +{bx}+\mathrm{1}\right) \\ $$$${and}\:{solve}\:{a}\:{and}\:{b} \\ $$
Answered by mathmax by abdo last updated on 27/May/20
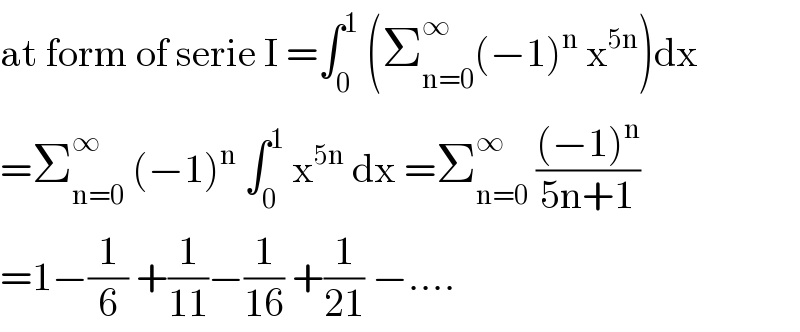
$$\mathrm{at}\:\mathrm{form}\:\mathrm{of}\:\mathrm{serie}\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{5n}} \right)\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{5n}} \:\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{5n}+\mathrm{1}} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}}\:+\frac{\mathrm{1}}{\mathrm{11}}−\frac{\mathrm{1}}{\mathrm{16}}\:+\frac{\mathrm{1}}{\mathrm{21}}\:−.... \\ $$
