Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 94857 by i jagooll last updated on 21/May/20

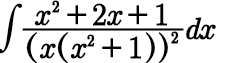
Commented by prakash jain last updated on 21/May/20

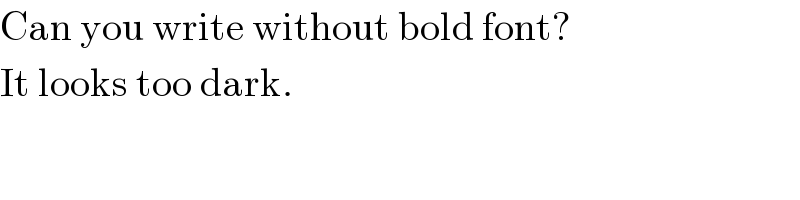
Can you write without bold font? It looks too dark.

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{write}\:\mathrm{without}\:\mathrm{bold}\:\mathrm{font}? \\ $$$$\mathrm{It}\:\mathrm{looks}\:\mathrm{too}\:\mathrm{dark}. \\ $$

Commented by i jagooll last updated on 21/May/20

on my cellphone it is not dark

Commented by i jagooll last updated on 21/May/20

and that's the result of the photo

Commented by mr W last updated on 21/May/20

you should try to crop your image properly, i.e. to keep more write space around the formula (in this case more write space on left and right side from the formula), then you will get properly sized image after posting. currently the images you posted look very tiny. this is an example what i do: tap your image and my image, you will see where the difference is.

$${you}\:{should}\:{try}\:{to}\:{crop}\:{your}\:{image} \\ $$$${properly},\:{i}.{e}.\:{to}\:{keep}\:{more}\:{write} \\ $$$${space}\:{around}\:{the}\:{formula}\:\left({in}\:{this}\right. \\ $$$${case}\:{more}\:{write}\:{space}\:{on}\:{left}\:{and}\:{right} \\ $$$$\left.{side}\:{from}\:{the}\:{formula}\right),\:{then}\:{you} \\ $$$${will}\:{get}\:{properly}\:{sized}\:{image}\:{after} \\ $$$${posting}.\:{currently}\:{the}\:{images}\:{you} \\ $$$${posted}\:{look}\:{very}\:{tiny}. \\ $$$${this}\:{is}\:{an}\:{example}\:{what}\:{i}\:{do}: \\ $$$${tap}\:{your}\:{image}\:{and}\:{my}\:{image},\:{you} \\ $$$${will}\:{see}\:{where}\:{the}\:{difference}\:{is}. \\ $$

Commented by mr W last updated on 21/May/20

Commented by mr W last updated on 21/May/20

i think i know how the problem comes. you write the formula with the editor of this app and then save it as image and then post it into the forum. but the editor saves the formula as image without any extra write space around the formula. if you don′t treat such an image with an other app, you won′t be able to solve this problem. but my question: why don′t you write the formula directly in the forum?

$${i}\:{think}\:{i}\:{know}\:{how}\:{the}\:{problem}\:{comes}. \\ $$$${you}\:{write}\:{the}\:{formula}\:{with}\:{the}\:{editor} \\ $$$${of}\:{this}\:{app}\:{and}\:{then}\:{save}\:{it}\:{as}\:{image} \\ $$$${and}\:{then}\:{post}\:{it}\:{into}\:{the}\:{forum}.\:{but} \\ $$$${the}\:{editor}\:{saves}\:{the}\:{formula}\:{as}\:{image} \\ $$$${without}\:{any}\:{extra}\:{write}\:{space}\:{around} \\ $$$${the}\:{formula}.\:{if}\:{you}\:{don}'{t}\:{treat}\:{such} \\ $$$${an}\:{image}\:{with}\:{an}\:{other}\:{app},\:{you} \\ $$$${won}'{t}\:{be}\:{able}\:{to}\:{solve}\:{this}\:{problem}. \\ $$$${but}\:{my}\:{question}:\:{why}\:{don}'{t}\:{you}\:{write} \\ $$$${the}\:{formula}\:{directly}\:{in}\:{the}\:{forum}? \\ $$

Commented by Tinku Tara last updated on 21/May/20

We reverted changes so that images will again be scaled to width. So they will look big. Please update to latest version. 2.71. We are still working on a proper solution for very small images. Thank You.

$$\mathrm{We}\:\mathrm{reverted}\:\mathrm{changes}\:\mathrm{so}\:\mathrm{that}\:\mathrm{images} \\ $$$$\mathrm{will}\:\mathrm{again}\:\mathrm{be}\:\mathrm{scaled}\:\mathrm{to}\:\mathrm{width}.\:\mathrm{So} \\ $$$$\mathrm{they}\:\mathrm{will}\:\mathrm{look}\:\mathrm{big}.\:\mathrm{Please}\:\mathrm{update} \\ $$$$\mathrm{to}\:\mathrm{latest}\:\mathrm{version}.\:\mathrm{2}.\mathrm{71}. \\ $$$$\mathrm{We}\:\mathrm{are}\:\mathrm{still}\:\mathrm{working}\:\mathrm{on}\:\mathrm{a}\:\mathrm{proper} \\ $$$$\mathrm{solution}\:\mathrm{for}\:\mathrm{very}\:\mathrm{small}\:\mathrm{images}. \\ $$$$\mathrm{Thank}\:\mathrm{You}. \\ $$

Answered by mathmax by abdo last updated on 21/May/20

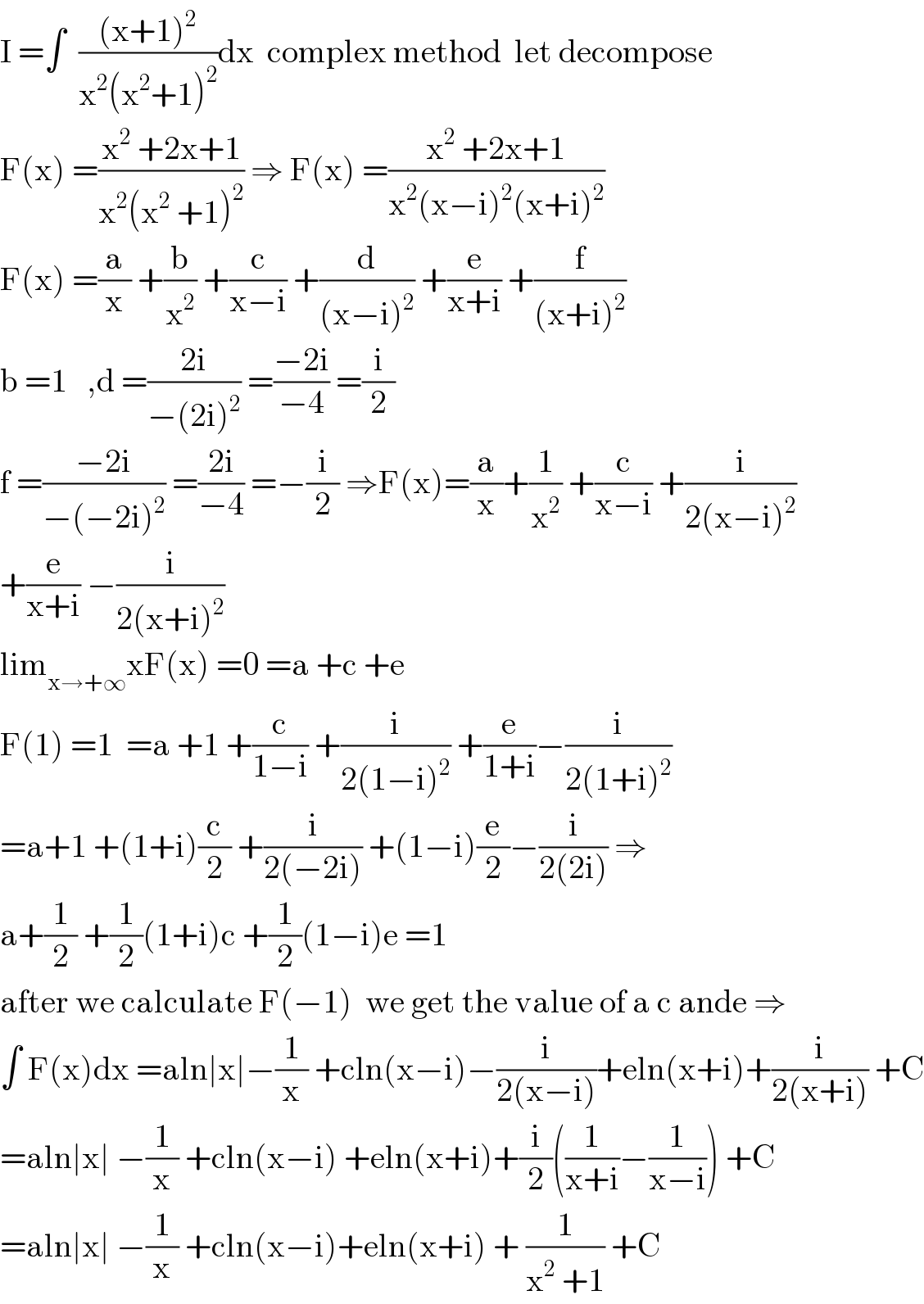
I =∫ (((x+1)^2 )/(x^2 (x^2 +1)^2 ))dx complex method let decompose F(x) =((x^2 +2x+1)/(x^2 (x^2 +1)^2 )) ⇒ F(x) =((x^2 +2x+1)/(x^2 (x−i)^2 (x+i)^2 )) F(x) =(a/x) +(b/x^2 ) +(c/(x−i)) +(d/((x−i)^2 )) +(e/(x+i)) +(f/((x+i)^2 )) b =1 ,d =((2i)/(−(2i)^2 )) =((−2i)/(−4)) =(i/2) f =((−2i)/(−(−2i)^2 )) =((2i)/(−4)) =−(i/2) ⇒F(x)=(a/x)+(1/x^2 ) +(c/(x−i)) +(i/(2(x−i)^2 )) +(e/(x+i)) −(i/(2(x+i)^2 )) lim_(x→+∞) xF(x) =0 =a +c +e F(1) =1 =a +1 +(c/(1−i)) +(i/(2(1−i)^2 )) +(e/(1+i))−(i/(2(1+i)^2 )) =a+1 +(1+i)(c/2) +(i/(2(−2i))) +(1−i)(e/2)−(i/(2(2i))) ⇒ a+(1/2) +(1/2)(1+i)c +(1/2)(1−i)e =1 after we calculate F(−1) we get the value of a c ande ⇒ ∫ F(x)dx =aln∣x∣−(1/x) +cln(x−i)−(i/(2(x−i)))+eln(x+i)+(i/(2(x+i))) +C =aln∣x∣ −(1/x) +cln(x−i) +eln(x+i)+(i/2)((1/(x+i))−(1/(x−i))) +C =aln∣x∣ −(1/x) +cln(x−i)+eln(x+i) + (1/(x^2 +1)) +C

$$\mathrm{I}\:=\int\:\:\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:\:\mathrm{complex}\:\mathrm{method}\:\:\mathrm{let}\:\mathrm{decompose} \\ $$$$\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\:\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\mathrm{i}\right)^{\mathrm{2}} \left(\mathrm{x}+\mathrm{i}\right)^{\mathrm{2}} } \\ $$$$\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{a}}{\mathrm{x}}\:+\frac{\mathrm{b}}{\mathrm{x}^{\mathrm{2}} }\:+\frac{\mathrm{c}}{\mathrm{x}−\mathrm{i}}\:+\frac{\mathrm{d}}{\left(\mathrm{x}−\mathrm{i}\right)^{\mathrm{2}} }\:+\frac{\mathrm{e}}{\mathrm{x}+\mathrm{i}}\:+\frac{\mathrm{f}}{\left(\mathrm{x}+\mathrm{i}\right)^{\mathrm{2}} } \\ $$$$\mathrm{b}\:=\mathrm{1}\:\:\:,\mathrm{d}\:=\frac{\mathrm{2i}}{−\left(\mathrm{2i}\right)^{\mathrm{2}} }\:=\frac{−\mathrm{2i}}{−\mathrm{4}}\:=\frac{\mathrm{i}}{\mathrm{2}} \\ $$$$\mathrm{f}\:=\frac{−\mathrm{2i}}{−\left(−\mathrm{2i}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2i}}{−\mathrm{4}}\:=−\frac{\mathrm{i}}{\mathrm{2}}\:\Rightarrow\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{a}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:+\frac{\mathrm{c}}{\mathrm{x}−\mathrm{i}}\:+\frac{\mathrm{i}}{\mathrm{2}\left(\mathrm{x}−\mathrm{i}\right)^{\mathrm{2}} } \\ $$$$+\frac{\mathrm{e}}{\mathrm{x}+\mathrm{i}}\:−\frac{\mathrm{i}}{\mathrm{2}\left(\mathrm{x}+\mathrm{i}\right)^{\mathrm{2}} } \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{xF}\left(\mathrm{x}\right)\:=\mathrm{0}\:=\mathrm{a}\:+\mathrm{c}\:+\mathrm{e} \\ $$$$\mathrm{F}\left(\mathrm{1}\right)\:=\mathrm{1}\:\:=\mathrm{a}\:+\mathrm{1}\:+\frac{\mathrm{c}}{\mathrm{1}−\mathrm{i}}\:+\frac{\mathrm{i}}{\mathrm{2}\left(\mathrm{1}−\mathrm{i}\right)^{\mathrm{2}} }\:+\frac{\mathrm{e}}{\mathrm{1}+\mathrm{i}}−\frac{\mathrm{i}}{\mathrm{2}\left(\mathrm{1}+\mathrm{i}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{a}+\mathrm{1}\:+\left(\mathrm{1}+\mathrm{i}\right)\frac{\mathrm{c}}{\mathrm{2}}\:+\frac{\mathrm{i}}{\mathrm{2}\left(−\mathrm{2i}\right)}\:+\left(\mathrm{1}−\mathrm{i}\right)\frac{\mathrm{e}}{\mathrm{2}}−\frac{\mathrm{i}}{\mathrm{2}\left(\mathrm{2i}\right)}\:\Rightarrow \\ $$$$\mathrm{a}+\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{i}\right)\mathrm{c}\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{i}\right)\mathrm{e}\:=\mathrm{1} \\ $$$$\mathrm{after}\:\mathrm{we}\:\mathrm{calculate}\:\mathrm{F}\left(−\mathrm{1}\right)\:\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{a}\:\mathrm{c}\:\mathrm{ande}\:\Rightarrow \\ $$$$\int\:\mathrm{F}\left(\mathrm{x}\right)\mathrm{dx}\:=\mathrm{aln}\mid\mathrm{x}\mid−\frac{\mathrm{1}}{\mathrm{x}}\:+\mathrm{cln}\left(\mathrm{x}−\mathrm{i}\right)−\frac{\mathrm{i}}{\mathrm{2}\left(\mathrm{x}−\mathrm{i}\right)}+\mathrm{eln}\left(\mathrm{x}+\mathrm{i}\right)+\frac{\mathrm{i}}{\mathrm{2}\left(\mathrm{x}+\mathrm{i}\right)}\:+\mathrm{C} \\ $$$$=\mathrm{aln}\mid\mathrm{x}\mid\:−\frac{\mathrm{1}}{\mathrm{x}}\:+\mathrm{cln}\left(\mathrm{x}−\mathrm{i}\right)\:+\mathrm{eln}\left(\mathrm{x}+\mathrm{i}\right)+\frac{\mathrm{i}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{x}+\mathrm{i}}−\frac{\mathrm{1}}{\mathrm{x}−\mathrm{i}}\right)\:+\mathrm{C} \\ $$$$=\mathrm{aln}\mid\mathrm{x}\mid\:−\frac{\mathrm{1}}{\mathrm{x}}\:+\mathrm{cln}\left(\mathrm{x}−\mathrm{i}\right)+\mathrm{eln}\left(\mathrm{x}+\mathrm{i}\right)\:+\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:+\mathrm{C} \\ $$

Answered by niroj last updated on 21/May/20

I= ∫ ((x^2 +2x+1)/({x(x^2 +1)}^2 ))dx = ∫ ((x^2 +1+2x)/(x^2 (x^2 +1)^2 ))dx = ∫ (( (x^2 +1))/(x^2 (x^2 +1)^2 ))dx +∫ (( 2x)/(x^2 (x^2 +1)^2 ))dx = ∫ (1/(x^2 (x^2 +1)))dx+∫ (( 2x)/(x^2 (x^2 +1)))dx I=I_1 +I_2 For, I_2 Put, x^2 +1=t , x^2 =t−1 2xdx=dt ∫(( 1)/x^2 )dx−∫(( 1)/(x^2 +1))dx+∫(1/((t−1)t))dt [ (x^(−2+1) /(−2+1))] −tan^(−1) x +∫(1/(t−1))dt−∫(1/t)dt+ C (x^(−1) /(−1)) − tan^(−1) x +log (t−1)−log t+C −(1/x) − tan^(−1) x +log ((t−1)/t) +C − (1/x)−tan^(−1) x + log ((x^2 +1−1)/(x^2 +1))+C −(1/x) −tan^(−1) x +log (x^2 /(x^2 +1))+C //.

$$\:\mathrm{I}=\:\int\:\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}}{\left\{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\right\}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\:\:\:=\:\int\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}+\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\:\:\:=\:\:\int\:\frac{\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:+\int\:\frac{\:\:\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\:=\:\int\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{dx}+\int\:\frac{\:\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{dx} \\ $$$$\:\:\mathrm{I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} \\ $$$$\:\:\mathrm{For},\:{I}_{\mathrm{2}} \\ $$$$\:\:\:\mathrm{Put},\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{t}\:,\:\mathrm{x}^{\mathrm{2}} =\mathrm{t}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{2xdx}=\mathrm{dt} \\ $$$$\:\:\int\frac{\:\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}−\int\frac{\:\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}+\int\frac{\mathrm{1}}{\left(\mathrm{t}−\mathrm{1}\right)\mathrm{t}}\mathrm{dt} \\ $$$$\:\:\:\left[\:\frac{\mathrm{x}^{−\mathrm{2}+\mathrm{1}} }{−\mathrm{2}+\mathrm{1}}\right]\:−\mathrm{tan}^{−\mathrm{1}} \mathrm{x}\:+\int\frac{\mathrm{1}}{\mathrm{t}−\mathrm{1}}\mathrm{dt}−\int\frac{\mathrm{1}}{\mathrm{t}}\mathrm{dt}+\:\mathrm{C} \\ $$$$\:\:\:\frac{\mathrm{x}^{−\mathrm{1}} }{−\mathrm{1}}\:−\:\mathrm{tan}^{−\mathrm{1}} \mathrm{x}\:+\mathrm{log}\:\left(\mathrm{t}−\mathrm{1}\right)−\mathrm{log}\:\mathrm{t}+\mathrm{C} \\ $$$$−\frac{\mathrm{1}}{\mathrm{x}}\:−\:\mathrm{tan}^{−\mathrm{1}} \mathrm{x}\:+\mathrm{log}\:\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}}\:+\mathrm{C} \\ $$$$\:−\:\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{tan}^{−\mathrm{1}} \mathrm{x}\:+\:\mathrm{log}\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}+\mathrm{C} \\ $$$$\:\:−\frac{\mathrm{1}}{\mathrm{x}}\:−\mathrm{tan}^{−\mathrm{1}} \mathrm{x}\:+\mathrm{log}\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}+\mathrm{C}\://. \\ $$$$\: \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com