
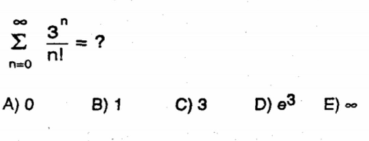
Question Number 94406 by Power last updated on 18/May/20
Commented by Tony Lin last updated on 18/May/20

$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!}={e}^{{x}} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{3}^{{n}} }{{n}!}={e}^{\mathrm{3}} \\ $$
Commented by Power last updated on 18/May/20
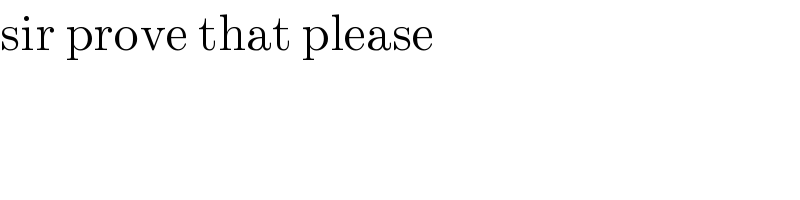
$$\mathrm{sir}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{please} \\ $$
Commented by prakash jain last updated on 18/May/20
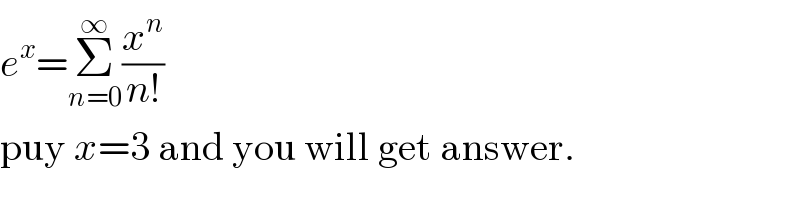
$${e}^{{x}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!} \\ $$$$\mathrm{puy}\:{x}=\mathrm{3}\:\mathrm{and}\:\mathrm{you}\:\mathrm{will}\:\mathrm{get}\:\mathrm{answer}. \\ $$
Commented by prakash jain last updated on 18/May/20
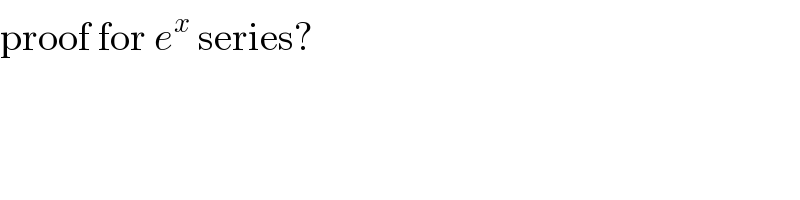
$$\mathrm{proof}\:\mathrm{for}\:{e}^{{x}} \:\mathrm{series}? \\ $$
Commented by MAB last updated on 18/May/20
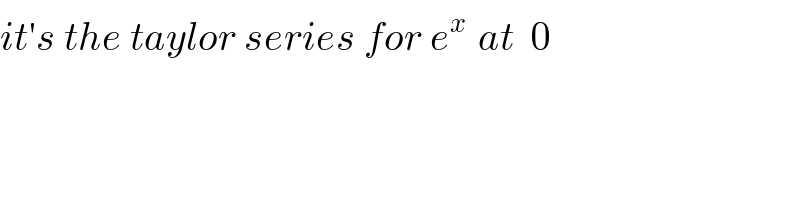
$${it}'{s}\:{the}\:{taylor}\:{series}\:{for}\:{e}^{{x}\:} \:{at}\:\:\mathrm{0} \\ $$
