
Question and Answers Forum
Question Number 92772 by Power last updated on 09/May/20
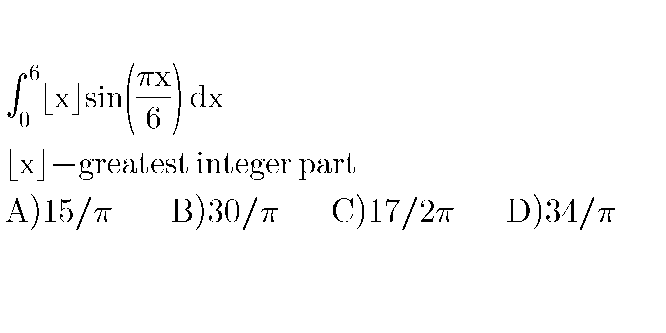
Commented by mathmax by abdo last updated on 09/May/20
![A =∫_0 ^6 [x] sin(((πx)/6))dx ⇒ A =Σ_(k=0) ^5 ∫_k ^(k+1) k sin(((πx)/6))dx =Σ_(k=0) ^5 k ∫_k ^(k+1) sin(((πx)/6))dx =Σ_(k=0) ^5 k [−(6/π)cos(((πx)/6))]_k ^(k+1) =−(6/π) Σ_(k=0) ^5 k{ cos(((π(k+1))/6))−cos(((kπ)/6))} =−(6/π)( cos((π/3))−cos((π/6))+cos((π/2))−cos((π/3))+cos(((2π)/3))−cos((π/2)) +cos(((5π)/6))−cos(((2π)/3)) +cos(π)−cos(((5π)/6))) =−(6/π){−((√3)/2)−(1/2) +(1/2) −1} =(6/π)(1+((√3)/2)) =(6/(2π))(1+(√3))](Q92911.png)
| ||
Question and Answers Forum | ||
Question Number 92772 by Power last updated on 09/May/20 | ||
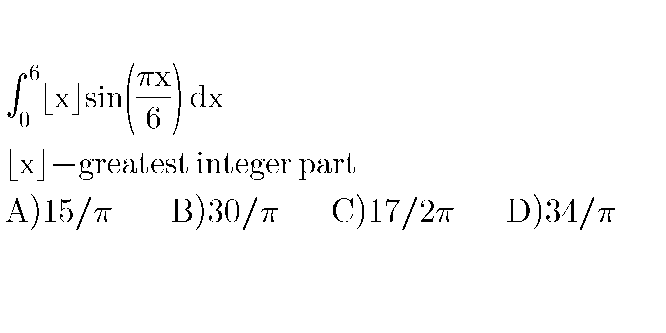 | ||
Commented by mathmax by abdo last updated on 09/May/20 | ||
![A =∫_0 ^6 [x] sin(((πx)/6))dx ⇒ A =Σ_(k=0) ^5 ∫_k ^(k+1) k sin(((πx)/6))dx =Σ_(k=0) ^5 k ∫_k ^(k+1) sin(((πx)/6))dx =Σ_(k=0) ^5 k [−(6/π)cos(((πx)/6))]_k ^(k+1) =−(6/π) Σ_(k=0) ^5 k{ cos(((π(k+1))/6))−cos(((kπ)/6))} =−(6/π)( cos((π/3))−cos((π/6))+cos((π/2))−cos((π/3))+cos(((2π)/3))−cos((π/2)) +cos(((5π)/6))−cos(((2π)/3)) +cos(π)−cos(((5π)/6))) =−(6/π){−((√3)/2)−(1/2) +(1/2) −1} =(6/π)(1+((√3)/2)) =(6/(2π))(1+(√3))](Q92911.png) | ||