
Question Number 90100 by ar247 last updated on 21/Apr/20
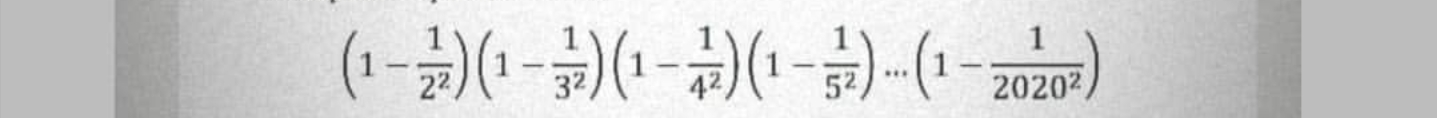
Answered by john santu last updated on 21/Apr/20
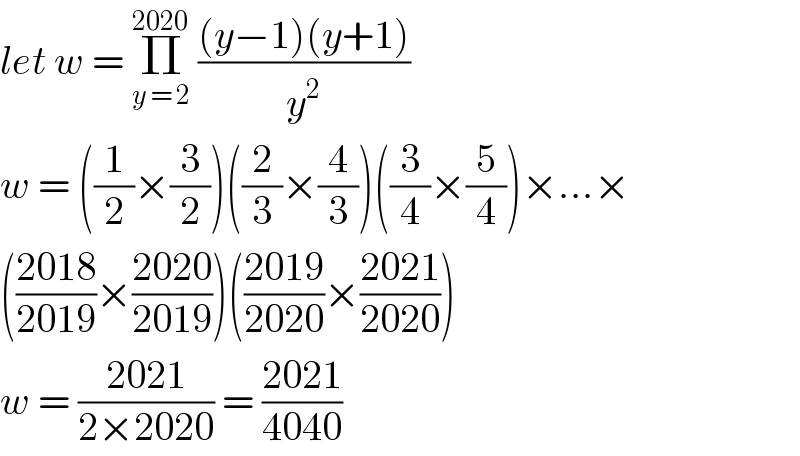
$${let}\:{w}\:=\:\underset{{y}\:=\:\mathrm{2}} {\overset{\mathrm{2020}} {\prod}}\:\frac{\left({y}−\mathrm{1}\right)\left({y}+\mathrm{1}\right)}{{y}^{\mathrm{2}} } \\ $$$${w}\:=\:\left(\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{2}}\right)\left(\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{4}}{\mathrm{3}}\right)\left(\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{5}}{\mathrm{4}}\right)×...× \\ $$$$\left(\frac{\mathrm{2018}}{\mathrm{2019}}×\frac{\mathrm{2020}}{\mathrm{2019}}\right)\left(\frac{\mathrm{2019}}{\mathrm{2020}}×\frac{\mathrm{2021}}{\mathrm{2020}}\right) \\ $$$${w}\:=\:\frac{\mathrm{2021}}{\mathrm{2}×\mathrm{2020}}\:=\:\frac{\mathrm{2021}}{\mathrm{4040}} \\ $$
Commented by Joel578 last updated on 21/Apr/20
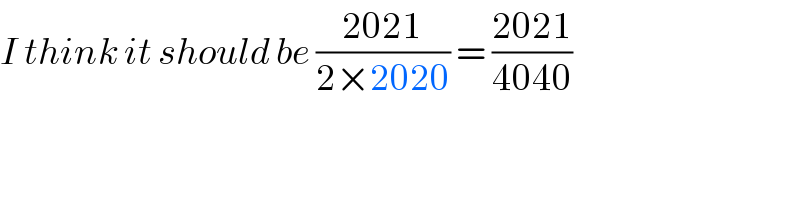
$${I}\:{think}\:{it}\:{should}\:{be}\:\frac{\mathrm{2021}}{\mathrm{2}×\mathrm{2020}}\:=\:\frac{\mathrm{2021}}{\mathrm{4040}} \\ $$
Commented by john santu last updated on 21/Apr/20

$${o}\:{yes}.\:{thank}\: \\ $$
