Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 89300 by I want to learn more last updated on 16/Apr/20

.

$$. \\ $$

Commented by I want to learn more last updated on 16/Apr/20

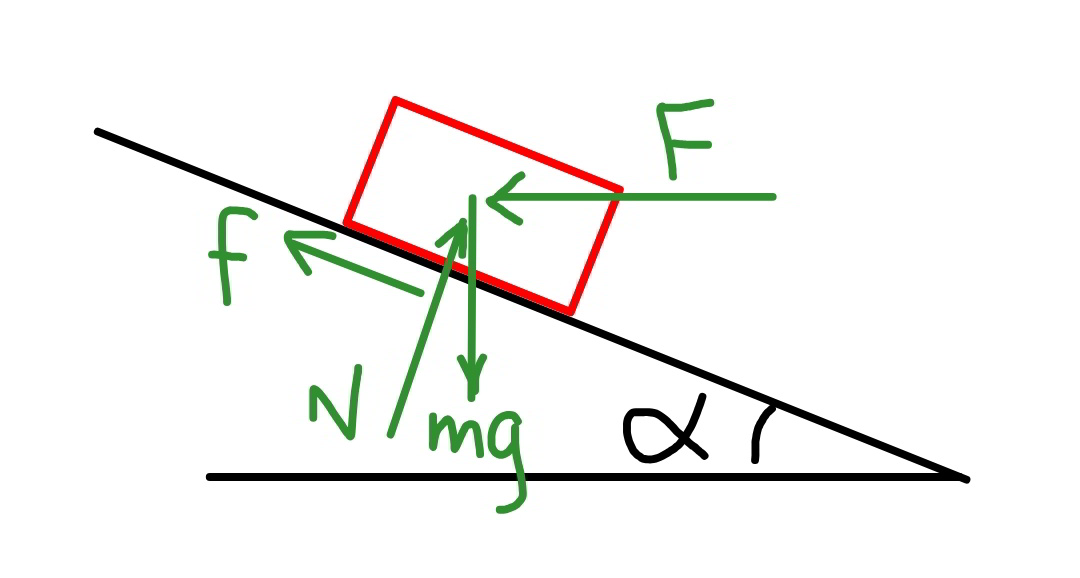
Determine the minimum horizontal force required to maintain a 10kg box on a ramp inclined at 30° to the horizontal if the coefficient of friction is 0.2

Commented by mr W last updated on 17/Apr/20

Commented by mr W last updated on 17/Apr/20

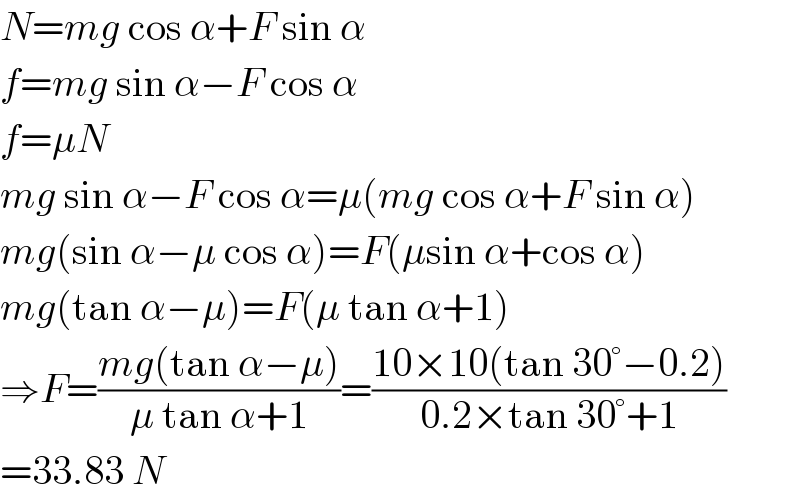
N=mg cos α+F sin α f=mg sin α−F cos α f=μN mg sin α−F cos α=μ(mg cos α+F sin α) mg(sin α−μ cos α)=F(μsin α+cos α) mg(tan α−μ)=F(μ tan α+1) ⇒F=((mg(tan α−μ))/(μ tan α+1))=((10×10(tan 30°−0.2))/(0.2×tan 30°+1)) =33.83 N

$${N}={mg}\:\mathrm{cos}\:\alpha+{F}\:\mathrm{sin}\:\alpha \\ $$$${f}={mg}\:\mathrm{sin}\:\alpha−{F}\:\mathrm{cos}\:\alpha \\ $$$${f}=\mu{N} \\ $$$${mg}\:\mathrm{sin}\:\alpha−{F}\:\mathrm{cos}\:\alpha=\mu\left({mg}\:\mathrm{cos}\:\alpha+{F}\:\mathrm{sin}\:\alpha\right) \\ $$$${mg}\left(\mathrm{sin}\:\alpha−\mu\:\mathrm{cos}\:\alpha\right)={F}\left(\mu\mathrm{sin}\:\alpha+\mathrm{cos}\:\alpha\right) \\ $$$${mg}\left(\mathrm{tan}\:\alpha−\mu\right)={F}\left(\mu\:\mathrm{tan}\:\alpha+\mathrm{1}\right) \\ $$$$\Rightarrow{F}=\frac{{mg}\left(\mathrm{tan}\:\alpha−\mu\right)}{\mu\:\mathrm{tan}\:\alpha+\mathrm{1}}=\frac{\mathrm{10}×\mathrm{10}\left(\mathrm{tan}\:\mathrm{30}°−\mathrm{0}.\mathrm{2}\right)}{\mathrm{0}.\mathrm{2}×\mathrm{tan}\:\mathrm{30}°+\mathrm{1}} \\ $$$$=\mathrm{33}.\mathrm{83}\:{N} \\ $$

Commented by I want to learn more last updated on 17/Apr/20

Thanks sir. I appreciate.

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Answered by 242242864 last updated on 17/Apr/20

Horizontal force = F Resolving along the plane Fcos ∝+uR=mgsin ∝.......(i) Vertically the plane, Fsin ∝+mgcos ∝=R ⇒Fcos ∝+u(Fsin ∝+mgcos ∝)=mgsin ∝ but ∝=30^° Fcos 30^° +0.2(Fsin 30^° +10×9.8cos 30°)=10×9.8sin 30^° 0.87F+0.1F+16.97=49 F= ((32.03)/(0.97)) F= 33.02N

$$\boldsymbol{{H}}{orizontal}\:{force}\:=\:\boldsymbol{{F}} \\ $$$$\boldsymbol{{R}}{esolving}\:{along}\:{the}\:{plane} \\ $$$$\boldsymbol{{F}}\mathrm{cos}\:\propto+\boldsymbol{{uR}}=\boldsymbol{{mg}}\mathrm{sin}\:\propto.......\left(\boldsymbol{{i}}\right) \\ $$$$\boldsymbol{{V}}{ertically}\:{the}\:{plane}, \\ $$$$\boldsymbol{{F}}\mathrm{sin}\:\propto+\boldsymbol{{mg}}\mathrm{cos}\:\propto=\boldsymbol{{R}} \\ $$$$\Rightarrow\boldsymbol{{F}}\mathrm{cos}\:\propto+\boldsymbol{{u}}\left(\boldsymbol{{F}}\mathrm{sin}\:\propto+\boldsymbol{{mg}}\mathrm{cos}\:\propto\right)=\boldsymbol{{mg}}\mathrm{sin}\:\propto \\ $$$${but}\:\propto=\mathrm{30}^{°} \\ $$$$\boldsymbol{{F}}\mathrm{cos}\:\mathrm{30}^{°} +\mathrm{0}.\mathrm{2}\left(\boldsymbol{{F}}\mathrm{sin}\:\mathrm{30}^{°} +\mathrm{10}×\mathrm{9}.\mathrm{8cos}\:\mathrm{30}°\right)=\mathrm{10}×\mathrm{9}.\mathrm{8sin}\:\mathrm{30}^{°} \\ $$$$\mathrm{0}.\mathrm{87}\boldsymbol{{F}}+\mathrm{0}.\mathrm{1}\boldsymbol{{F}}+\mathrm{16}.\mathrm{97}=\mathrm{49} \\ $$$$\boldsymbol{{F}}=\:\frac{\mathrm{32}.\mathrm{03}}{\mathrm{0}.\mathrm{97}} \\ $$$$\boldsymbol{{F}}=\:\mathrm{33}.\mathrm{02}\boldsymbol{{N}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by I want to learn more last updated on 17/Apr/20

Thanks sir, i appreciate

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com