
Question Number 88918 by mathocean1 last updated on 13/Apr/20

Commented by mathocean1 last updated on 13/Apr/20
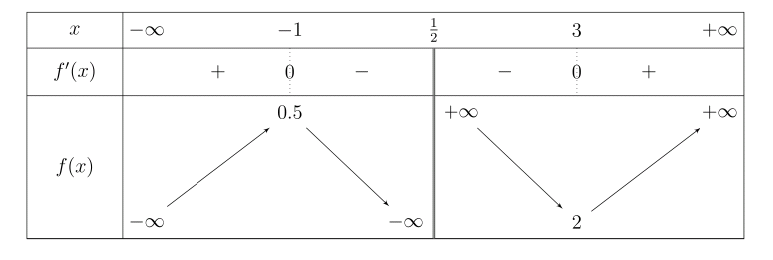
Commented by mathocean1 last updated on 13/Apr/20
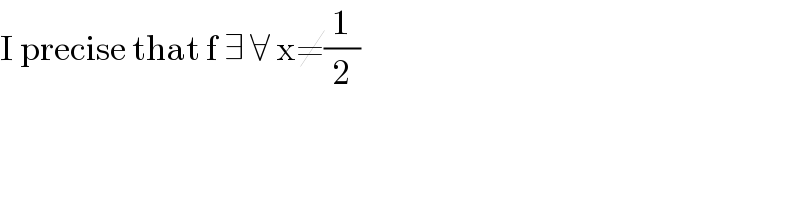
$$\mathrm{I}\:\mathrm{precise}\:\mathrm{that}\:\mathrm{f}\:\exists\:\forall\:\mathrm{x}\neq\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 13/Apr/20
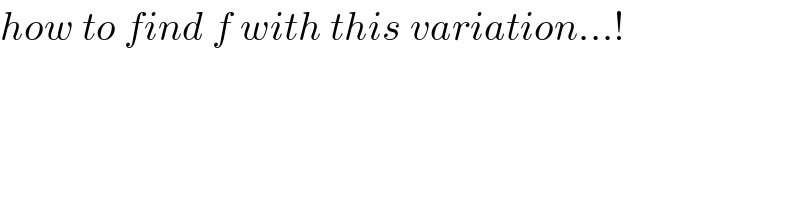
$${how}\:{to}\:{find}\:{f}\:{with}\:{this}\:{variation}...! \\ $$
Commented by mathocean1 last updated on 14/Apr/20

$$\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{also}\:\mathrm{know} \\ $$
Commented by MJS last updated on 14/Apr/20
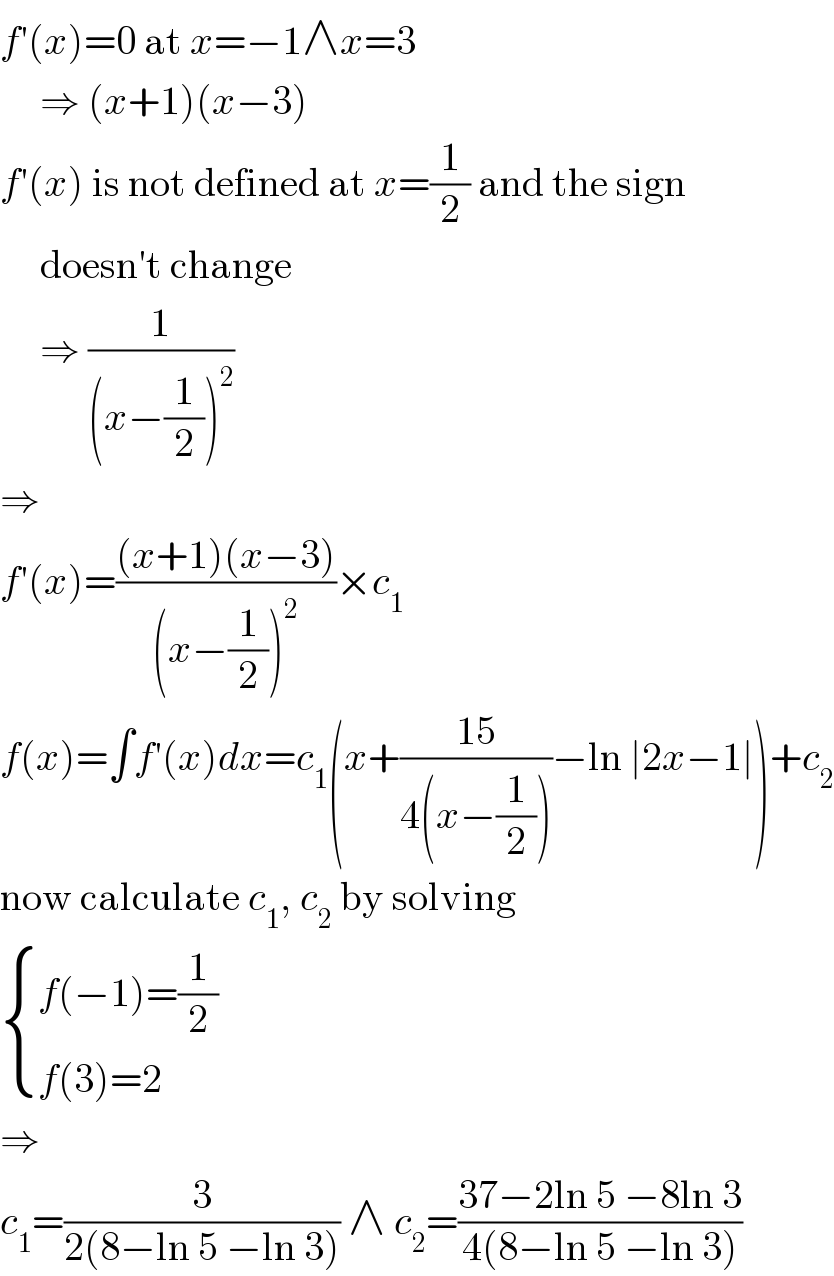
$${f}'\left({x}\right)=\mathrm{0}\:\mathrm{at}\:{x}=−\mathrm{1}\wedge{x}=\mathrm{3} \\ $$$$\:\:\:\:\:\Rightarrow\:\left({x}+\mathrm{1}\right)\left({x}−\mathrm{3}\right) \\ $$$${f}'\left({x}\right)\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{at}\:{x}=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{the}\:\mathrm{sign} \\ $$$$\:\:\:\:\:\mathrm{doesn}'\mathrm{t}\:\mathrm{change} \\ $$$$\:\:\:\:\:\Rightarrow\:\frac{\mathrm{1}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow \\ $$$${f}'\left({x}\right)=\frac{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{3}\right)}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }×{c}_{\mathrm{1}} \\ $$$${f}\left({x}\right)=\int{f}'\left({x}\right){dx}={c}_{\mathrm{1}} \left({x}+\frac{\mathrm{15}}{\mathrm{4}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)}−\mathrm{ln}\:\mid\mathrm{2}{x}−\mathrm{1}\mid\right)+{c}_{\mathrm{2}} \\ $$$$\mathrm{now}\:\mathrm{calculate}\:{c}_{\mathrm{1}} ,\:{c}_{\mathrm{2}} \:\mathrm{by}\:\mathrm{solving} \\ $$$$\begin{cases}{{f}\left(−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}}\\{{f}\left(\mathrm{3}\right)=\mathrm{2}}\end{cases} \\ $$$$\Rightarrow \\ $$$${c}_{\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{2}\left(\mathrm{8}−\mathrm{ln}\:\mathrm{5}\:−\mathrm{ln}\:\mathrm{3}\right)}\:\wedge\:{c}_{\mathrm{2}} =\frac{\mathrm{37}−\mathrm{2ln}\:\mathrm{5}\:−\mathrm{8ln}\:\mathrm{3}}{\mathrm{4}\left(\mathrm{8}−\mathrm{ln}\:\mathrm{5}\:−\mathrm{ln}\:\mathrm{3}\right)} \\ $$
Commented by mathocean1 last updated on 14/Apr/20
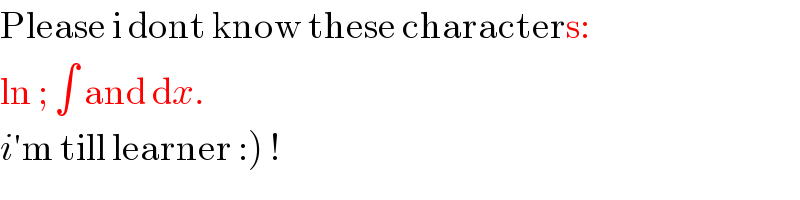
$$\mathrm{Please}\:\mathrm{i}\:\mathrm{dont}\:\mathrm{know}\:\mathrm{these}\:\mathrm{characters}: \\ $$$$\mathrm{ln}\:;\:\int\:\mathrm{and}\:\mathrm{d}{x}. \\ $$$$\left.{i}'\mathrm{m}\:\mathrm{till}\:\mathrm{learner}\::\right)\:! \\ $$
Commented by MJS last updated on 14/Apr/20

$$\mathrm{how}\:\mathrm{come}\:\mathrm{you}\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{a}\:\mathrm{question}\:\mathrm{like} \\ $$$$\mathrm{this}\:\mathrm{without}\:\mathrm{knowing}\:\mathrm{these}\:\mathrm{symbols}??? \\ $$$$\mathrm{I}\:\mathrm{cannot}\:\mathrm{explain}\:\mathrm{this}\:\mathrm{within}\:\mathrm{a}\:\mathrm{comment},\:\mathrm{it} \\ $$$$\mathrm{needs}\:\mathrm{teaching}\:\mathrm{for}\:\mathrm{months} \\ $$
Commented by mathocean1 last updated on 15/Apr/20

$$\mathrm{alright}. \\ $$
Commented by MJS last updated on 15/Apr/20

$$\mathrm{sorry}\:\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{want}\:\mathrm{to}\:\mathrm{be}\:\mathrm{impolite} \\ $$$$\mathrm{I}\:\mathrm{cannot}\:\mathrm{see}\:\mathrm{an}\:\mathrm{easier}\:\mathrm{path}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this} \\ $$$$\mathrm{problem}.\:\mathrm{in}\:\mathrm{Austria},\:\mathrm{we}\:\mathrm{have}\:\mathrm{12}\:\mathrm{years}\:\mathrm{of} \\ $$$$\mathrm{school},\:\mathrm{you}\:\mathrm{learn}\:``\mathrm{ln}''\:\mathrm{in}\:\mathrm{the}\:\mathrm{10}^{\mathrm{th}} \:\mathrm{year}\:\mathrm{and} \\ $$$$``\int{dx}''\:\mathrm{in}\:\mathrm{the}\:\mathrm{12}^{\mathrm{th}} \:\mathrm{year}... \\ $$$$\mathrm{just}\:\mathrm{to}\:\mathrm{give}\:\mathrm{you}\:\mathrm{a}\:\mathrm{picture} \\ $$
Commented by mathocean1 last updated on 08/Jun/20

$${thanks}\:{sir} \\ $$
