Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

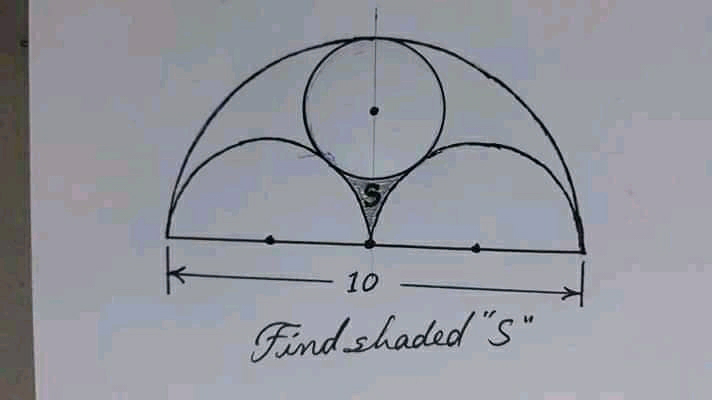
Question Number 86789 by TawaTawa1 last updated on 31/Mar/20

Commented by jagoll last updated on 31/Mar/20

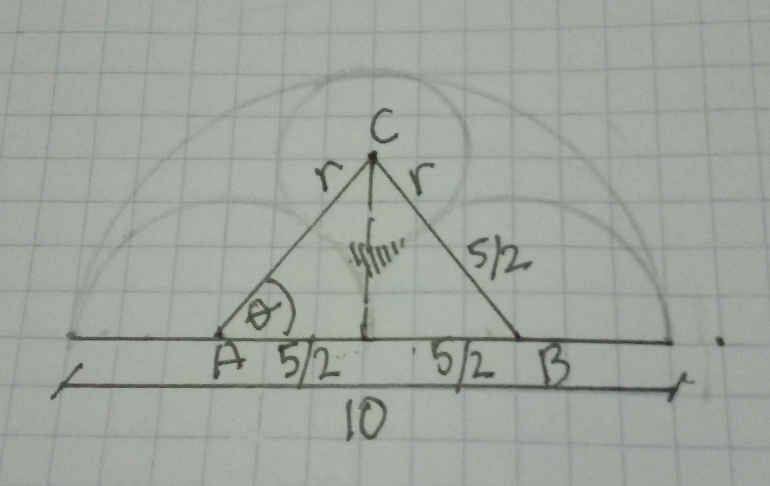
Answered by jagoll last updated on 31/Mar/20

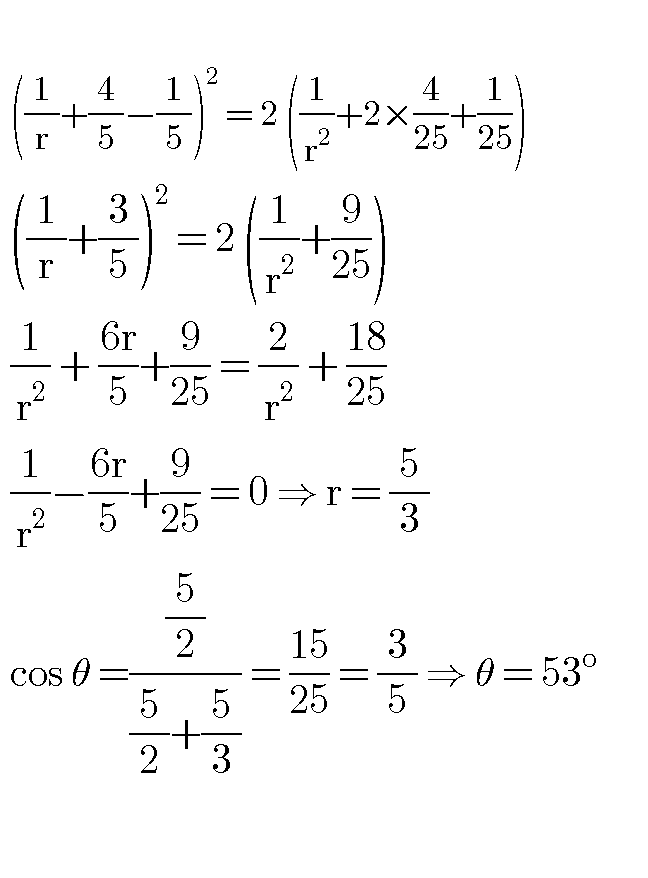
Commented by jagoll last updated on 31/Mar/20

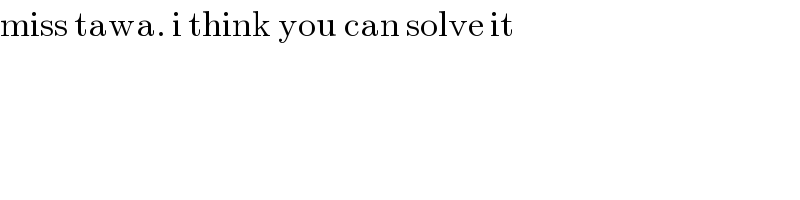
miss tawa. i think you can solve it

$$\mathrm{miss}\:\mathrm{tawa}.\:\mathrm{i}\:\mathrm{think}\:\mathrm{you}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{it} \\ $$

Commented by TawaTawa1 last updated on 31/Mar/20

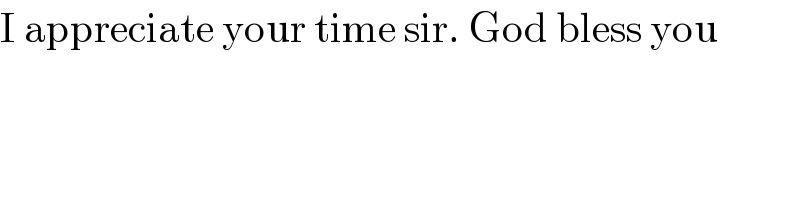
I appreciate your time sir. God bless you

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$

Commented by TawaTawa1 last updated on 31/Mar/20

I did not understand the first step.

$$\mathrm{I}\:\mathrm{did}\:\mathrm{not}\:\mathrm{understand}\:\mathrm{the}\:\mathrm{first}\:\mathrm{step}. \\ $$

Commented by jagoll last updated on 31/Mar/20

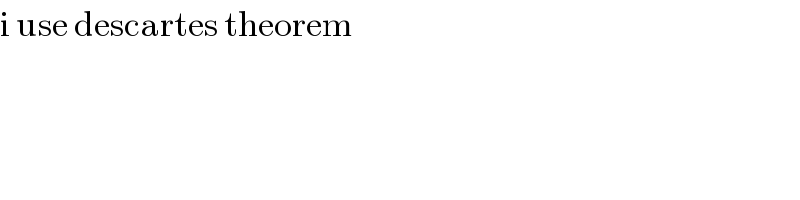
i use descartes theorem

$$\mathrm{i}\:\mathrm{use}\:\mathrm{descartes}\:\mathrm{theorem} \\ $$

Commented by TawaTawa1 last updated on 31/Mar/20

But sir, you have not find the area. What is the area sir please. Area of the shaded

$$\mathrm{But}\:\mathrm{sir},\:\mathrm{you}\:\mathrm{have}\:\mathrm{not}\:\mathrm{find}\:\mathrm{the}\:\mathrm{area}. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{area}\:\mathrm{sir}\:\mathrm{please}. \\ $$$$\mathrm{Area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{shaded} \\ $$

Commented by jagoll last updated on 31/Mar/20

the area can already be calculated by substracting the area of the triangle with the area of the circle

$$\mathrm{the}\:\mathrm{area}\:\mathrm{can}\:\mathrm{already}\:\mathrm{be}\:\mathrm{calculated} \\ $$$$\mathrm{by}\:\mathrm{substracting}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\: \\ $$$$\mathrm{triangle}\:\mathrm{with}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle} \\ $$

Commented by TawaTawa1 last updated on 31/Mar/20

The three circle?

$$\mathrm{The}\:\mathrm{three}\:\mathrm{circle}? \\ $$

Commented by TawaTawa1 last updated on 01/Apr/20

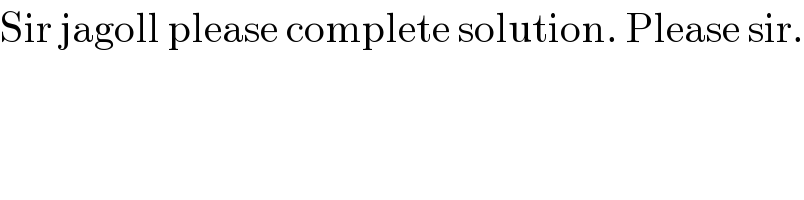
Sir jagoll please complete solution. Please sir.

$$\mathrm{Sir}\:\mathrm{jagoll}\:\mathrm{please}\:\mathrm{complete}\:\mathrm{solution}.\:\mathrm{Please}\:\mathrm{sir}. \\ $$

Commented by jagoll last updated on 01/Apr/20

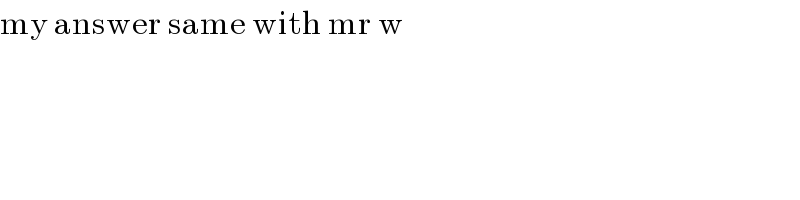
my answer same with mr w

$$\mathrm{my}\:\mathrm{answer}\:\mathrm{same}\:\mathrm{with}\:\mathrm{mr}\:\mathrm{w}\: \\ $$

Answered by mr W last updated on 31/Mar/20

((5/2))^2 +(5−r)^2 =((5/2)+r)^2 ⇒r=(5/3) tan θ=((5−(5/3))/(5/2))=(4/3) A_(shaded) =((5(5−(5/3)))/2)−2×(1/2)((5/2))^2 θ−(1/2)((5/3))^2 (π−2θ) =((25)/3)−((25)/4)θ−(1/2)×((25)/9)(π−2θ) =((25)/(36))(12−2π−5θ) =((25)/(36))(12−2π−5 tan^(−1) (4/3))

$$\left(\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\mathrm{5}−{r}\right)^{\mathrm{2}} =\left(\frac{\mathrm{5}}{\mathrm{2}}+{r}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{5}−\frac{\mathrm{5}}{\mathrm{3}}}{\frac{\mathrm{5}}{\mathrm{2}}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${A}_{{shaded}} =\frac{\mathrm{5}\left(\mathrm{5}−\frac{\mathrm{5}}{\mathrm{3}}\right)}{\mathrm{2}}−\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} \theta−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{5}}{\mathrm{3}}\right)^{\mathrm{2}} \left(\pi−\mathrm{2}\theta\right) \\ $$$$=\frac{\mathrm{25}}{\mathrm{3}}−\frac{\mathrm{25}}{\mathrm{4}}\theta−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{25}}{\mathrm{9}}\left(\pi−\mathrm{2}\theta\right) \\ $$$$=\frac{\mathrm{25}}{\mathrm{36}}\left(\mathrm{12}−\mathrm{2}\pi−\mathrm{5}\theta\right) \\ $$$$=\frac{\mathrm{25}}{\mathrm{36}}\left(\mathrm{12}−\mathrm{2}\pi−\mathrm{5}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$

Commented by TawaTawa1 last updated on 31/Mar/20

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by TawaTawa1 last updated on 01/Apr/20

Sir i got − 180.51 when i press calculator. Can the area be negative or there is a mistake somewhere.

$$\mathrm{Sir}\:\mathrm{i}\:\mathrm{got}\:\:\:−\:\mathrm{180}.\mathrm{51}\:\:\:\mathrm{when}\:\mathrm{i}\:\mathrm{press}\:\mathrm{calculator}. \\ $$$$\mathrm{Can}\:\mathrm{the}\:\mathrm{area}\:\mathrm{be}\:\mathrm{negative}\:\mathrm{or}\:\mathrm{there}\:\mathrm{is}\:\mathrm{a}\:\mathrm{mistake}\:\mathrm{somewhere}. \\ $$

Commented by mr W last updated on 01/Apr/20

sorry. i can′t teach you how to use calculator. it seems you don′t make difference between rad and degree, i just guess.

$${sorry}.\:{i}\:{can}'{t}\:{teach}\:{you}\:{how}\:{to}\:{use}\: \\ $$$${calculator}.\:{it}\:{seems}\:{you}\:{don}'{t}\:{make} \\ $$$${difference}\:{between}\:{rad}\:{and}\:{degree}, \\ $$$${i}\:{just}\:{guess}. \\ $$

Commented by john santu last updated on 01/Apr/20

= 0.750235

$$=\:\mathrm{0}.\mathrm{750235} \\ $$

Commented by TawaTawa1 last updated on 01/Apr/20

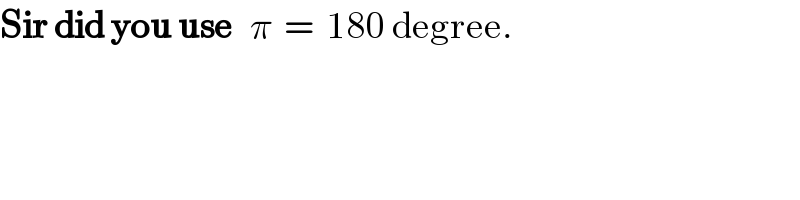
Sir did you use π = 180 degree.

$$\boldsymbol{\mathrm{Sir}}\:\boldsymbol{\mathrm{did}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{use}}\:\:\:\pi\:\:=\:\:\mathrm{180}\:\mathrm{degree}. \\ $$

Commented by john santu last updated on 01/Apr/20

Commented by TawaTawa1 last updated on 01/Apr/20

Ohh. You work in radian sir. I appreciate.

$$\mathrm{Ohh}.\:\mathrm{You}\:\mathrm{work}\:\mathrm{in}\:\mathrm{radian}\:\mathrm{sir}.\:\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Commented by TawaTawa1 last updated on 01/Apr/20

Am sorry sir mrW. I press i work in degree.

$$\mathrm{Am}\:\mathrm{sorry}\:\mathrm{sir}\:\:\mathrm{mrW}.\:\:\mathrm{I}\:\mathrm{press}\:\mathrm{i}\:\mathrm{work}\:\mathrm{in}\:\mathrm{degree}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com