
Question Number 86610 by TawaTawa1 last updated on 29/Mar/20
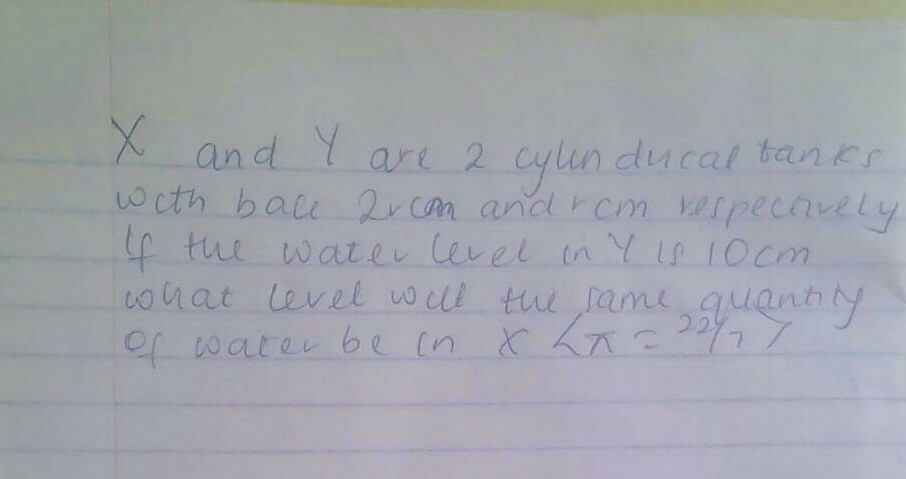
Commented by TawaTawa1 last updated on 29/Mar/20
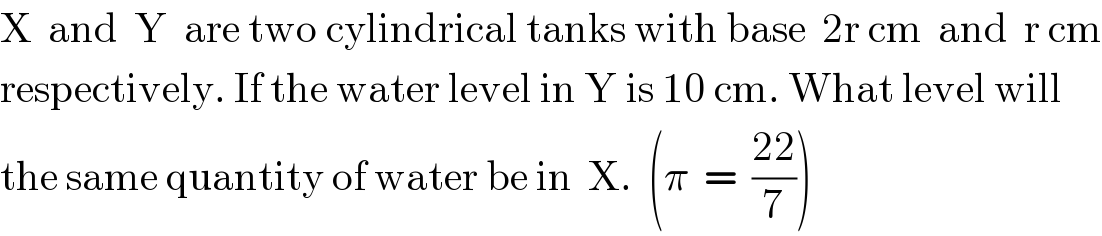
$$\mathrm{X}\:\:\mathrm{and}\:\:\mathrm{Y}\:\:\mathrm{are}\:\mathrm{two}\:\mathrm{cylindrical}\:\mathrm{tanks}\:\mathrm{with}\:\mathrm{base}\:\:\mathrm{2r}\:\mathrm{cm}\:\:\mathrm{and}\:\:\mathrm{r}\:\mathrm{cm} \\ $$$$\mathrm{respectively}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{water}\:\mathrm{level}\:\mathrm{in}\:\mathrm{Y}\:\mathrm{is}\:\mathrm{10}\:\mathrm{cm}.\:\mathrm{What}\:\mathrm{level}\:\mathrm{will} \\ $$$$\mathrm{the}\:\mathrm{same}\:\mathrm{quantity}\:\mathrm{of}\:\mathrm{water}\:\mathrm{be}\:\mathrm{in}\:\:\mathrm{X}.\:\:\left(\pi\:\:=\:\:\frac{\mathrm{22}}{\mathrm{7}}\right) \\ $$
Commented by TawaTawa1 last updated on 29/Mar/20

$$\mathrm{I}\:\mathrm{got}\:\:\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$
Commented by jagoll last updated on 29/Mar/20
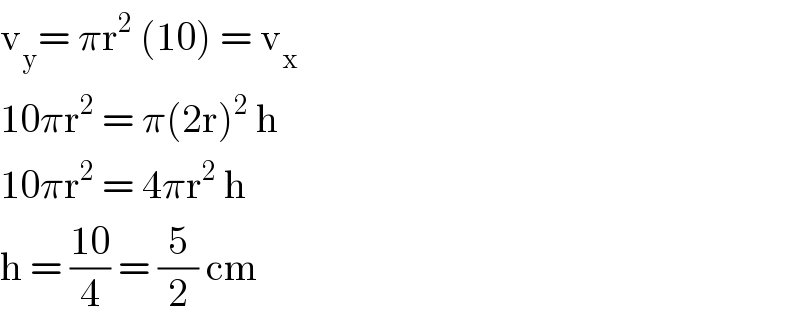
$$\mathrm{v}_{\mathrm{y}} =\:\pi\mathrm{r}^{\mathrm{2}} \:\left(\mathrm{10}\right)\:=\:\mathrm{v}_{\mathrm{x}} \\ $$$$\mathrm{10}\pi\mathrm{r}^{\mathrm{2}} \:=\:\pi\left(\mathrm{2r}\right)^{\mathrm{2}} \:\mathrm{h} \\ $$$$\mathrm{10}\pi\mathrm{r}^{\mathrm{2}} \:=\:\mathrm{4}\pi\mathrm{r}^{\mathrm{2}} \:\mathrm{h}\: \\ $$$$\mathrm{h}\:=\:\frac{\mathrm{10}}{\mathrm{4}}\:=\:\frac{\mathrm{5}}{\mathrm{2}}\:\mathrm{cm}\: \\ $$
Commented by TawaTawa1 last updated on 30/Mar/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
