
Question Number 86586 by Power last updated on 29/Mar/20
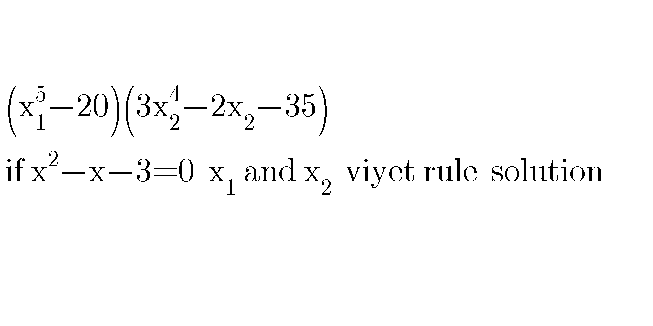
Commented by Power last updated on 29/Mar/20
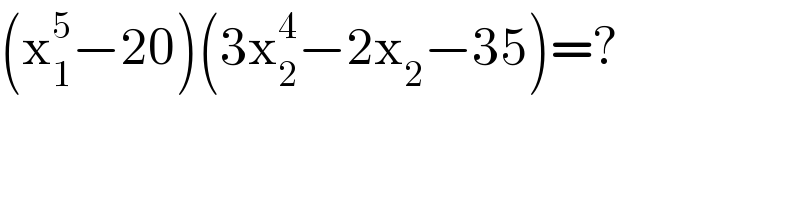
$$\left(\mathrm{x}_{\mathrm{1}} ^{\mathrm{5}} −\mathrm{20}\right)\left(\mathrm{3x}_{\mathrm{2}} ^{\mathrm{4}} −\mathrm{2x}_{\mathrm{2}} −\mathrm{35}\right)=? \\ $$
Commented by MJS last updated on 29/Mar/20
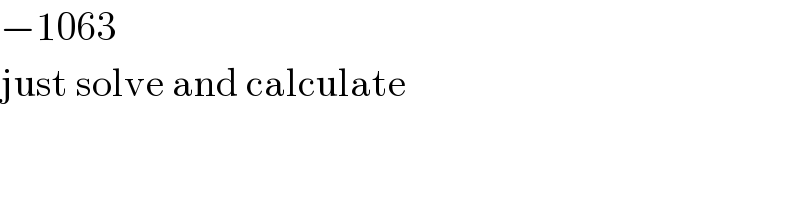
$$−\mathrm{1063} \\ $$$$\mathrm{just}\:\mathrm{solve}\:\mathrm{and}\:\mathrm{calculate} \\ $$
Commented by jagoll last updated on 29/Mar/20

$$\mathrm{wow}...\mathrm{super}\:\mathrm{easy} \\ $$
Commented by Power last updated on 29/Mar/20

$$\mathrm{prove}\:\mathrm{that}\:\mathrm{sir} \\ $$
Answered by lémùst last updated on 29/Mar/20
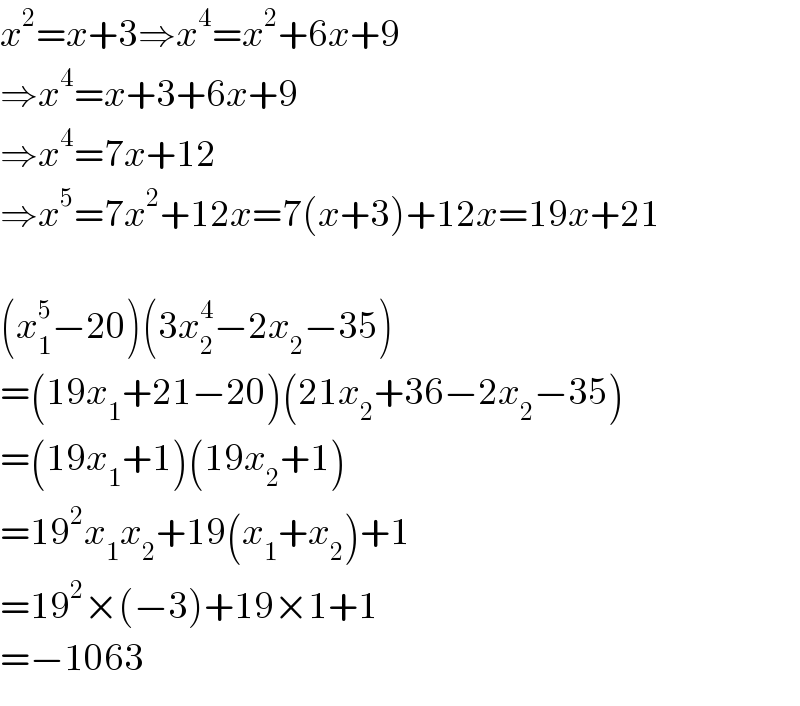
$${x}^{\mathrm{2}} ={x}+\mathrm{3}\Rightarrow{x}^{\mathrm{4}} ={x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{9} \\ $$$$\Rightarrow{x}^{\mathrm{4}} ={x}+\mathrm{3}+\mathrm{6}{x}+\mathrm{9} \\ $$$$\Rightarrow{x}^{\mathrm{4}} =\mathrm{7}{x}+\mathrm{12} \\ $$$$\Rightarrow{x}^{\mathrm{5}} =\mathrm{7}{x}^{\mathrm{2}} +\mathrm{12}{x}=\mathrm{7}\left({x}+\mathrm{3}\right)+\mathrm{12}{x}=\mathrm{19}{x}+\mathrm{21} \\ $$$$ \\ $$$$\left({x}_{\mathrm{1}} ^{\mathrm{5}} −\mathrm{20}\right)\left(\mathrm{3}{x}_{\mathrm{2}} ^{\mathrm{4}} −\mathrm{2}{x}_{\mathrm{2}} −\mathrm{35}\right) \\ $$$$=\left(\mathrm{19}{x}_{\mathrm{1}} +\mathrm{21}−\mathrm{20}\right)\left(\mathrm{21}{x}_{\mathrm{2}} +\mathrm{36}−\mathrm{2}{x}_{\mathrm{2}} −\mathrm{35}\right) \\ $$$$=\left(\mathrm{19}{x}_{\mathrm{1}} +\mathrm{1}\right)\left(\mathrm{19}{x}_{\mathrm{2}} +\mathrm{1}\right) \\ $$$$=\mathrm{19}^{\mathrm{2}} {x}_{\mathrm{1}} {x}_{\mathrm{2}} +\mathrm{19}\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)+\mathrm{1} \\ $$$$=\mathrm{19}^{\mathrm{2}} ×\left(−\mathrm{3}\right)+\mathrm{19}×\mathrm{1}+\mathrm{1} \\ $$$$=−\mathrm{1063} \\ $$
Commented by Power last updated on 29/Mar/20

$$\mathrm{thanks} \\ $$
Commented by lémùst last updated on 29/Mar/20

$${you}'{re}\:{welcome} \\ $$
