Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 86346 by Power last updated on 28/Mar/20

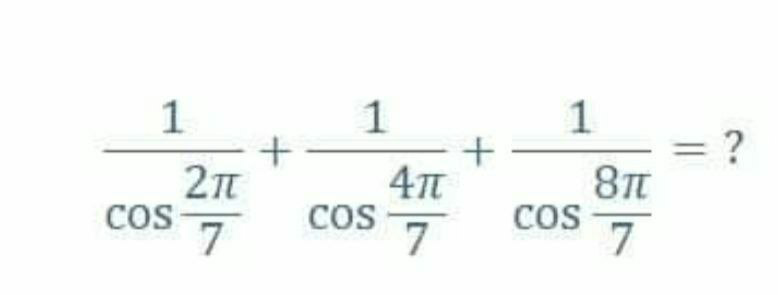
Commented by MJS last updated on 28/Mar/20

−4

$$−\mathrm{4} \\ $$

Commented by jagoll last updated on 28/Mar/20

yes.....i got the same result sir

$$\mathrm{yes}.....\mathrm{i}\:\mathrm{got}\:\mathrm{the}\:\mathrm{same}\:\mathrm{result}\:\mathrm{sir} \\ $$

Answered by TANMAY PANACEA. last updated on 28/Mar/20

7θ=2π 4θ=2π−3θ cos4θ=cos(2π−3θ) 2cos^2 2θ−1=4cos^3 θ−3cosθ 2(2cos^2 θ−1)^2 −1=4cos^3 θ−3cosθ 2(2x^2 −1)^2 −1=4x^3 −3x 2(4x^4 −4x^2 +1)−4x^3 +3x−1=0 8x^4 −4x^3 −8x^2 +3x+1=0 8x^4 −8x^3 +4x^3 −4x^2 −4x^2 +4x−x+1 8x^3 (x−1)+4x^2 (x−1)−4x(x−1)−1(x−1)=0 (x−1)(8x^3 +4x^2 −4x−1)=0 now look 8x^3 +4x^2 −4x−1=0 has three root and one root is cosθ cos(((2π)/7)) another cos(((4π)/7)) and cos(((6π)/7)) cos(((2π)/7))+cos(((4π)/7))+cos(((6π)/7))=((−4)/8)=((−1)/2) Σcos(((2π)/7))cos(((4π)/7))=((−4)/8)=((−1)/2) cos(((2π)/7))cos(((4π)/7))cos(((6π)/7))=(1/8) (1/(cos(((2π)/7))))+(1/(cos(((4π)/7))))+(1/(cos(((8π)/7)))) look... cos(((8π)/7))=cos(π+(π/7))=−cos((π/7)) cos(((6π)/7))=cos(π−(π/7))=−cos((π/7)) so cos(((6π)/7))=cos(((8π)/7)) (1/(cos(((2π)/7))))+(1/(cos(((4π)/7))))+(1/(cos(((8π)/7)))) =(1/(cos(((2π)/7))))+(1/(cos(((4π)/7))))+(1/(cos(((6π)/7)))) =((Σcos(((2π)/7))cos(((4π)/7)))/(cos(((2π)/7))cos(((4π)/7))cos(((6π)/7)))) =(((−1)/2)/(1/8))=−4

$$\mathrm{7}\theta=\mathrm{2}\pi \\ $$$$\mathrm{4}\theta=\mathrm{2}\pi−\mathrm{3}\theta \\ $$$${cos}\mathrm{4}\theta={cos}\left(\mathrm{2}\pi−\mathrm{3}\theta\right) \\ $$$$\mathrm{2}{cos}^{\mathrm{2}} \mathrm{2}\theta−\mathrm{1}=\mathrm{4}{cos}^{\mathrm{3}} \theta−\mathrm{3}{cos}\theta \\ $$$$\mathrm{2}\left(\mathrm{2}{cos}^{\mathrm{2}} \theta−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}=\mathrm{4}{cos}^{\mathrm{3}} \theta−\mathrm{3}{cos}\theta \\ $$$$\mathrm{2}\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}=\mathrm{4}{x}^{\mathrm{3}} −\mathrm{3}{x} \\ $$$$\mathrm{2}\left(\mathrm{4}{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{4}{x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{8}{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} −\mathrm{8}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{8}{x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}−{x}+\mathrm{1} \\ $$$$\mathrm{8}{x}^{\mathrm{3}} \left({x}−\mathrm{1}\right)+\mathrm{4}{x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)−\mathrm{4}{x}\left({x}−\mathrm{1}\right)−\mathrm{1}\left({x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left(\mathrm{8}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{1}\right)=\mathrm{0} \\ $$$${now}\:{look}\:\mathrm{8}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{1}=\mathrm{0} \\ $$$${has}\:{three}\:{root}\:{and}\:{one}\:{root}\:{is}\:{cos}\theta \\ $$$$\boldsymbol{{cos}}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)\:{another}\:{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)\:{and}\:{cos}\left(\frac{\mathrm{6}\pi}{\mathrm{7}}\right) \\ $$$${cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)+{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)+{cos}\left(\frac{\mathrm{6}\pi}{\mathrm{7}}\right)=\frac{−\mathrm{4}}{\mathrm{8}}=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$$$\Sigma{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right){cos}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)=\frac{−\mathrm{4}}{\mathrm{8}}=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$$${cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right){cos}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right){cos}\left(\frac{\mathrm{6}\pi}{\mathrm{7}}\right)=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\frac{\mathrm{1}}{{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)}+\frac{\mathrm{1}}{{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)}+\frac{\mathrm{1}}{{cos}\left(\frac{\mathrm{8}\pi}{\mathrm{7}}\right)} \\ $$$${look}... \\ $$$${cos}\left(\frac{\mathrm{8}\pi}{\mathrm{7}}\right)={cos}\left(\pi+\frac{\pi}{\mathrm{7}}\right)=−{cos}\left(\frac{\pi}{\mathrm{7}}\right) \\ $$$${cos}\left(\frac{\mathrm{6}\pi}{\mathrm{7}}\right)={cos}\left(\pi−\frac{\pi}{\mathrm{7}}\right)=−{cos}\left(\frac{\pi}{\mathrm{7}}\right) \\ $$$${so}\:{cos}\left(\frac{\mathrm{6}\pi}{\mathrm{7}}\right)={cos}\left(\frac{\mathrm{8}\pi}{\mathrm{7}}\right) \\ $$$$\frac{\mathrm{1}}{{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)}+\frac{\mathrm{1}}{{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)}+\frac{\mathrm{1}}{{cos}\left(\frac{\mathrm{8}\pi}{\mathrm{7}}\right)} \\ $$$$=\frac{\mathrm{1}}{{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right)}+\frac{\mathrm{1}}{{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)}+\frac{\mathrm{1}}{{cos}\left(\frac{\mathrm{6}\pi}{\mathrm{7}}\right)} \\ $$$$=\frac{\Sigma{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right){cos}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right)}{{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{7}}\right){cos}\left(\frac{\mathrm{4}\pi}{\mathrm{7}}\right){cos}\left(\frac{\mathrm{6}\pi}{\mathrm{7}}\right)} \\ $$$$=\frac{\frac{−\mathrm{1}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{8}}}=−\mathrm{4} \\ $$$$ \\ $$

Commented by Power last updated on 28/Mar/20

step by step solution sir

$$\mathrm{step}\:\mathrm{by}\:\mathrm{step}\:\mathrm{solution}\:\mathrm{sir} \\ $$

Commented by jagoll last updated on 28/Mar/20

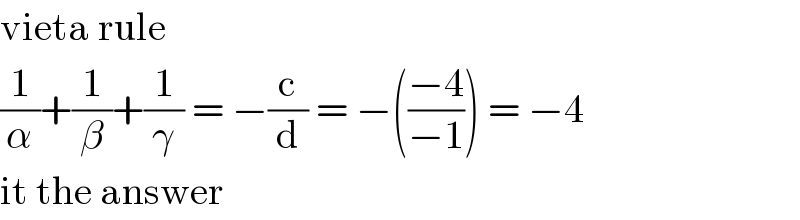
vieta rule (1/α)+(1/β)+(1/γ) = −(c/d) = −(((−4)/(−1))) = −4 it the answer

$$\mathrm{vieta}\:\mathrm{rule} \\ $$$$\frac{\mathrm{1}}{\alpha}+\frac{\mathrm{1}}{\beta}+\frac{\mathrm{1}}{\gamma}\:=\:−\frac{\mathrm{c}}{\mathrm{d}}\:=\:−\left(\frac{−\mathrm{4}}{−\mathrm{1}}\right)\:=\:−\mathrm{4} \\ $$$$\mathrm{it}\:\mathrm{the}\:\mathrm{answer} \\ $$

Commented by MJS last updated on 28/Mar/20

any steps by yourself Sir Power?

$$\mathrm{any}\:\mathrm{steps}\:\mathrm{by}\:\mathrm{yourself}\:\mathrm{Sir}\:\mathrm{Power}? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com