
Question Number 8618 by Rasheed Soomro last updated on 18/Oct/16
Commented by Rasheed Soomro last updated on 18/Oct/16
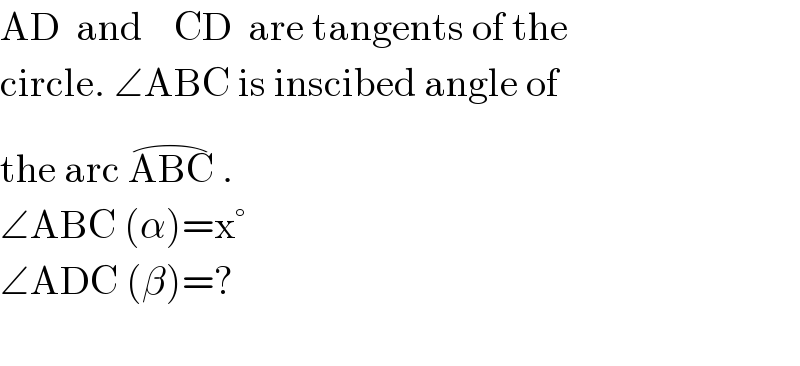
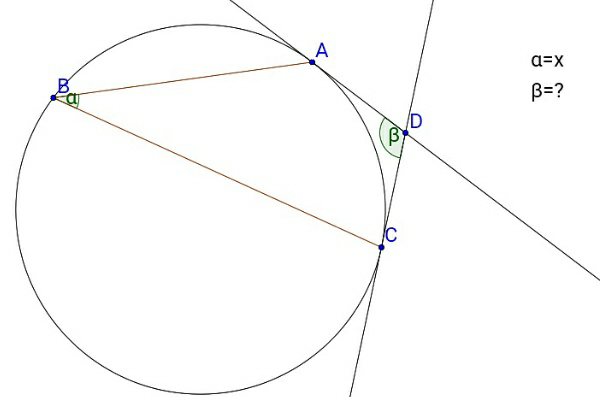
$$\mathrm{AD}\:\:\mathrm{and}\:\:\:\:\mathrm{CD}\:\:\mathrm{are}\:\mathrm{tangents}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{circle}.\:\angle\mathrm{ABC}\:\mathrm{is}\:\mathrm{inscibed}\:\mathrm{angle}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{arc}\:\overset{\frown} {\mathrm{ABC}}\:. \\ $$$$\angle\mathrm{ABC}\:\left(\alpha\right)=\mathrm{x}° \\ $$$$\angle\mathrm{ADC}\:\left(\beta\right)=? \\ $$$$ \\ $$
Answered by sandy_suhendra last updated on 18/Oct/16
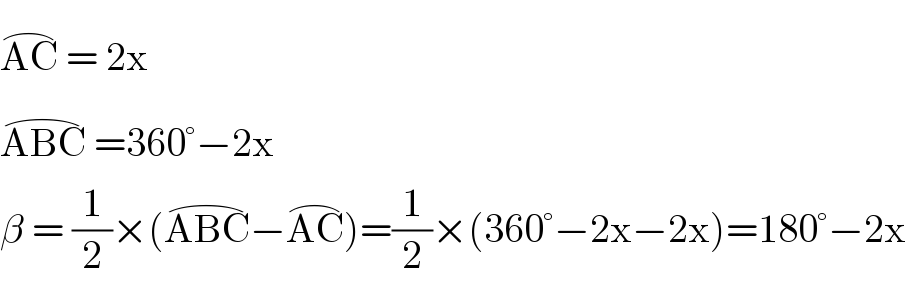
$$\overset{\frown} {\mathrm{AC}}\:=\:\mathrm{2x} \\ $$$$\overset{\frown} {\mathrm{ABC}}\:=\mathrm{360}°−\mathrm{2x} \\ $$$$\beta\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\left(\overset{\frown} {\mathrm{ABC}}−\overset{\frown} {\mathrm{AC}}\right)=\frac{\mathrm{1}}{\mathrm{2}}×\left(\mathrm{360}°−\mathrm{2x}−\mathrm{2x}\right)=\mathrm{180}°−\mathrm{2x} \\ $$
