Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 84941 by Power last updated on 17/Mar/20

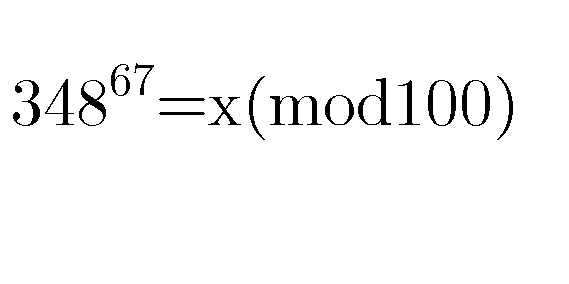
Commented by mr W last updated on 17/Mar/20

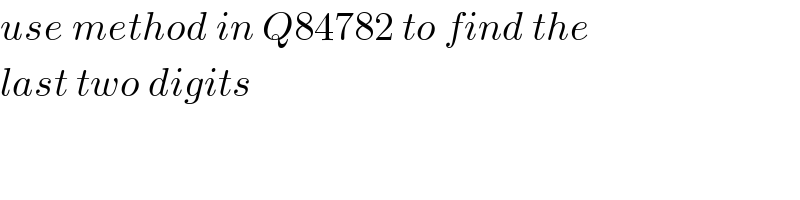
use method in Q84782 to find the last two digits

$${use}\:{method}\:{in}\:{Q}\mathrm{84782}\:{to}\:{find}\:{the} \\ $$$${last}\:{two}\:{digits} \\ $$

Answered by mr W last updated on 17/Mar/20

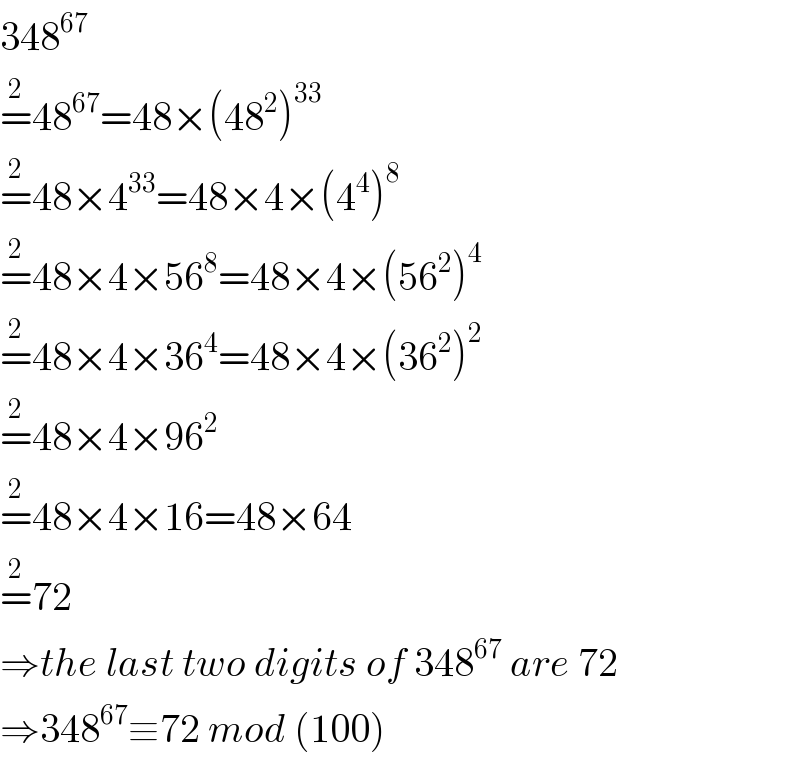
348^(67) =^2 48^(67) =48×(48^2 )^(33) =^2 48×4^(33) =48×4×(4^4 )^8 =^2 48×4×56^8 =48×4×(56^2 )^4 =^2 48×4×36^4 =48×4×(36^2 )^2 =^2 48×4×96^2 =^2 48×4×16=48×64 =^2 72 ⇒the last two digits of 348^(67) are 72 ⇒348^(67) ≡72 mod (100)

$$\mathrm{348}^{\mathrm{67}} \\ $$$$\overset{\mathrm{2}} {=}\mathrm{48}^{\mathrm{67}} =\mathrm{48}×\left(\mathrm{48}^{\mathrm{2}} \right)^{\mathrm{33}} \\ $$$$\overset{\mathrm{2}} {=}\mathrm{48}×\mathrm{4}^{\mathrm{33}} =\mathrm{48}×\mathrm{4}×\left(\mathrm{4}^{\mathrm{4}} \right)^{\mathrm{8}} \\ $$$$\overset{\mathrm{2}} {=}\mathrm{48}×\mathrm{4}×\mathrm{56}^{\mathrm{8}} =\mathrm{48}×\mathrm{4}×\left(\mathrm{56}^{\mathrm{2}} \right)^{\mathrm{4}} \\ $$$$\overset{\mathrm{2}} {=}\mathrm{48}×\mathrm{4}×\mathrm{36}^{\mathrm{4}} =\mathrm{48}×\mathrm{4}×\left(\mathrm{36}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\overset{\mathrm{2}} {=}\mathrm{48}×\mathrm{4}×\mathrm{96}^{\mathrm{2}} \\ $$$$\overset{\mathrm{2}} {=}\mathrm{48}×\mathrm{4}×\mathrm{16}=\mathrm{48}×\mathrm{64} \\ $$$$\overset{\mathrm{2}} {=}\mathrm{72} \\ $$$$\Rightarrow{the}\:{last}\:{two}\:{digits}\:{of}\:\mathrm{348}^{\mathrm{67}} \:{are}\:\mathrm{72} \\ $$$$\Rightarrow\mathrm{348}^{\mathrm{67}} \equiv\mathrm{72}\:{mod}\:\left(\mathrm{100}\right) \\ $$

Answered by mr W last updated on 18/Mar/20

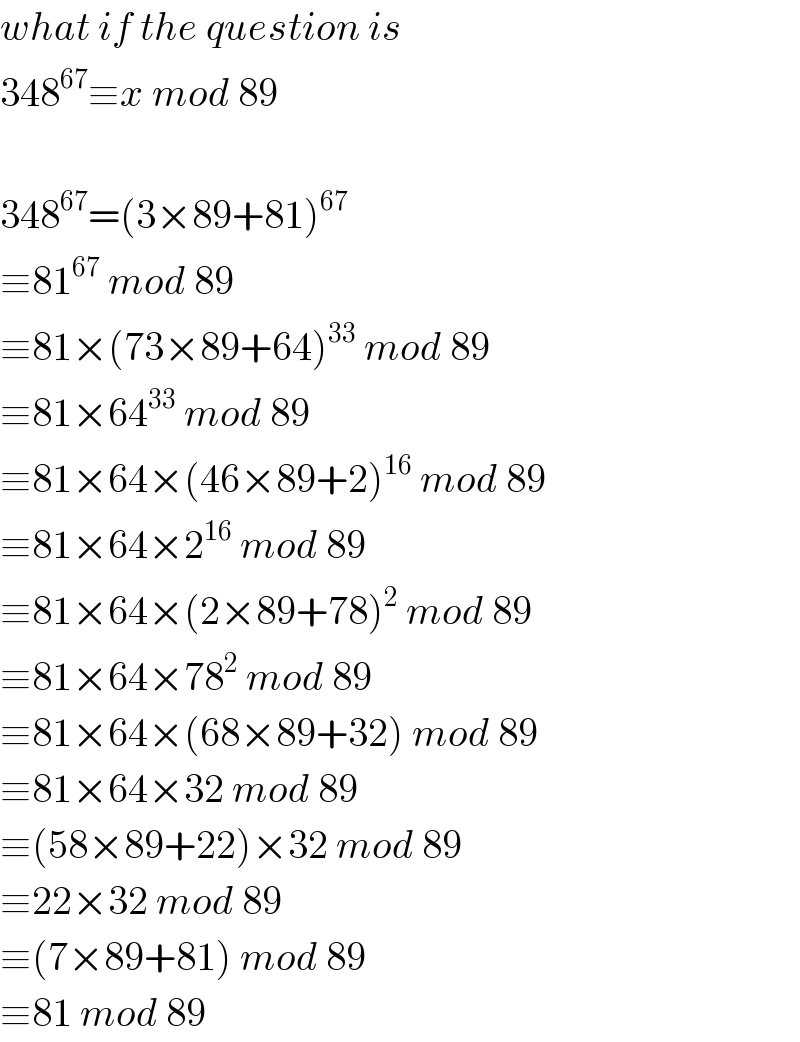
what if the question is 348^(67) ≡x mod 89 348^(67) =(3×89+81)^(67) ≡81^(67) mod 89 ≡81×(73×89+64)^(33) mod 89 ≡81×64^(33) mod 89 ≡81×64×(46×89+2)^(16) mod 89 ≡81×64×2^(16) mod 89 ≡81×64×(2×89+78)^2 mod 89 ≡81×64×78^2 mod 89 ≡81×64×(68×89+32) mod 89 ≡81×64×32 mod 89 ≡(58×89+22)×32 mod 89 ≡22×32 mod 89 ≡(7×89+81) mod 89 ≡81 mod 89

$${what}\:{if}\:{the}\:{question}\:{is} \\ $$$$\mathrm{348}^{\mathrm{67}} \equiv{x}\:{mod}\:\mathrm{89} \\ $$$$ \\ $$$$\mathrm{348}^{\mathrm{67}} =\left(\mathrm{3}×\mathrm{89}+\mathrm{81}\right)^{\mathrm{67}} \\ $$$$\equiv\mathrm{81}^{\mathrm{67}} \:{mod}\:\mathrm{89} \\ $$$$\equiv\mathrm{81}×\left(\mathrm{73}×\mathrm{89}+\mathrm{64}\right)^{\mathrm{33}} \:{mod}\:\mathrm{89} \\ $$$$\equiv\mathrm{81}×\mathrm{64}^{\mathrm{33}} \:{mod}\:\mathrm{89} \\ $$$$\equiv\mathrm{81}×\mathrm{64}×\left(\mathrm{46}×\mathrm{89}+\mathrm{2}\right)^{\mathrm{16}} \:{mod}\:\mathrm{89} \\ $$$$\equiv\mathrm{81}×\mathrm{64}×\mathrm{2}^{\mathrm{16}} \:{mod}\:\mathrm{89} \\ $$$$\equiv\mathrm{81}×\mathrm{64}×\left(\mathrm{2}×\mathrm{89}+\mathrm{78}\right)^{\mathrm{2}} \:{mod}\:\mathrm{89} \\ $$$$\equiv\mathrm{81}×\mathrm{64}×\mathrm{78}^{\mathrm{2}} \:{mod}\:\mathrm{89} \\ $$$$\equiv\mathrm{81}×\mathrm{64}×\left(\mathrm{68}×\mathrm{89}+\mathrm{32}\right)\:{mod}\:\mathrm{89} \\ $$$$\equiv\mathrm{81}×\mathrm{64}×\mathrm{32}\:{mod}\:\mathrm{89} \\ $$$$\equiv\left(\mathrm{58}×\mathrm{89}+\mathrm{22}\right)×\mathrm{32}\:{mod}\:\mathrm{89} \\ $$$$\equiv\mathrm{22}×\mathrm{32}\:{mod}\:\mathrm{89} \\ $$$$\equiv\left(\mathrm{7}×\mathrm{89}+\mathrm{81}\right)\:{mod}\:\mathrm{89} \\ $$$$\equiv\mathrm{81}\:{mod}\:\mathrm{89} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com