
Question Number 84894 by Power last updated on 17/Mar/20
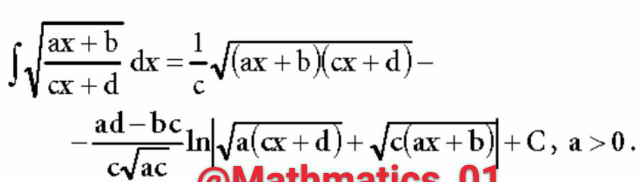
Commented by abdomathmax last updated on 18/Mar/20
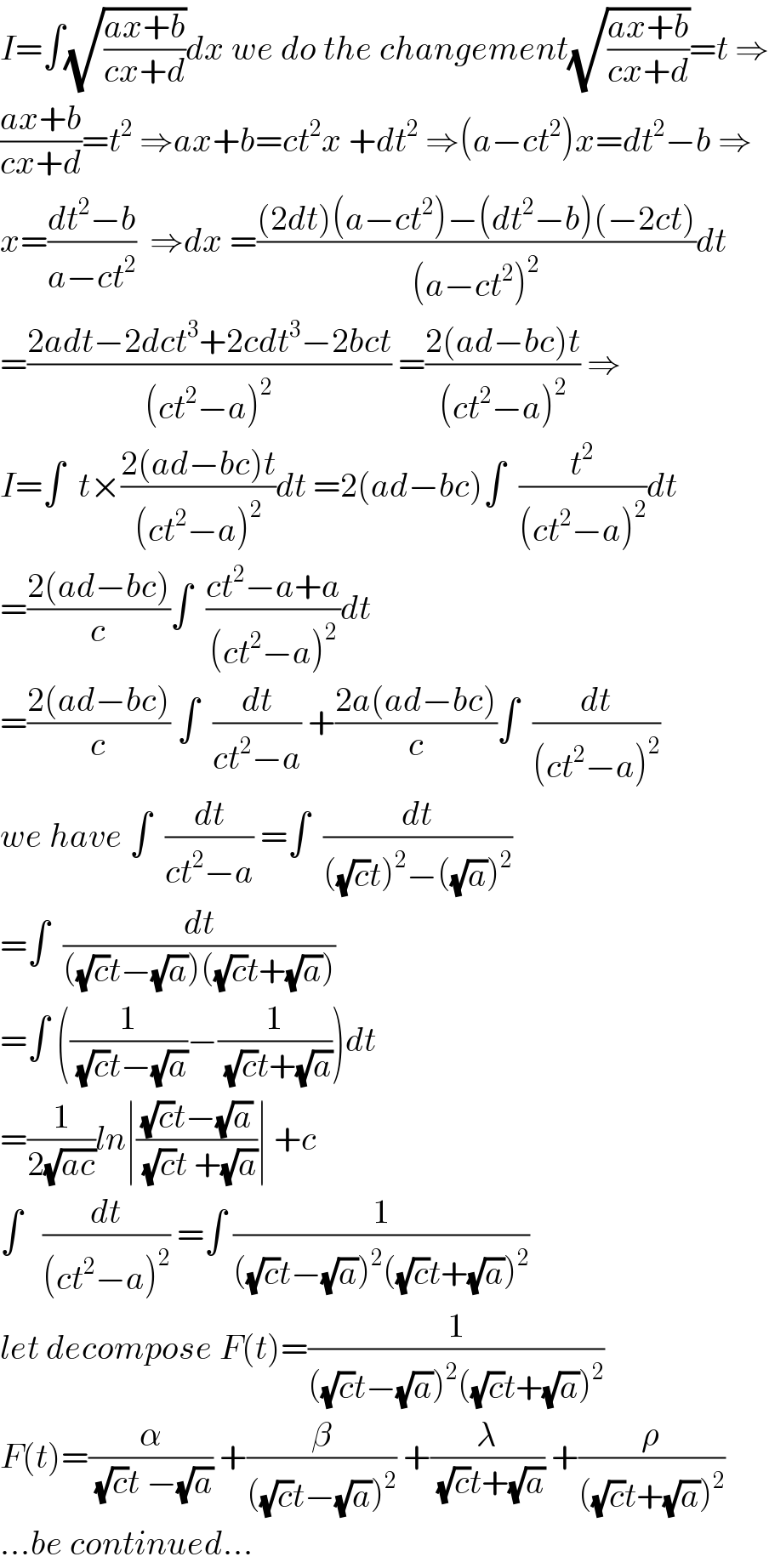
$${I}=\int\sqrt{\frac{{ax}+{b}}{{cx}+{d}}}{dx}\:{we}\:{do}\:{the}\:{changement}\sqrt{\frac{{ax}+{b}}{{cx}+{d}}}={t}\:\Rightarrow \\ $$$$\frac{{ax}+{b}}{{cx}+{d}}={t}^{\mathrm{2}} \:\Rightarrow{ax}+{b}={ct}^{\mathrm{2}} {x}\:+{dt}^{\mathrm{2}} \:\Rightarrow\left({a}−{ct}^{\mathrm{2}} \right){x}={dt}^{\mathrm{2}} −{b}\:\Rightarrow \\ $$$${x}=\frac{{dt}^{\mathrm{2}} −{b}}{{a}−{ct}^{\mathrm{2}} }\:\:\Rightarrow{dx}\:=\frac{\left(\mathrm{2}{dt}\right)\left({a}−{ct}^{\mathrm{2}} \right)−\left({dt}^{\mathrm{2}} −{b}\right)\left(−\mathrm{2}{ct}\right)}{\left({a}−{ct}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{2}{adt}−\mathrm{2}{dct}^{\mathrm{3}} +\mathrm{2}{cdt}^{\mathrm{3}} −\mathrm{2}{bct}}{\left({ct}^{\mathrm{2}} −{a}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2}\left({ad}−{bc}\right){t}}{\left({ct}^{\mathrm{2}} −{a}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}=\int\:\:{t}×\frac{\mathrm{2}\left({ad}−{bc}\right){t}}{\left({ct}^{\mathrm{2}} −{a}\right)^{\mathrm{2}} }{dt}\:=\mathrm{2}\left({ad}−{bc}\right)\int\:\:\frac{{t}^{\mathrm{2}} }{\left({ct}^{\mathrm{2}} −{a}\right)^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{2}\left({ad}−{bc}\right)}{{c}}\int\:\:\frac{{ct}^{\mathrm{2}} −{a}+{a}}{\left({ct}^{\mathrm{2}} −{a}\right)^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{2}\left({ad}−{bc}\right)}{{c}}\:\int\:\:\frac{{dt}}{{ct}^{\mathrm{2}} −{a}}\:+\frac{\mathrm{2}{a}\left({ad}−{bc}\right)}{{c}}\int\:\:\frac{{dt}}{\left({ct}^{\mathrm{2}} −{a}\right)^{\mathrm{2}} } \\ $$$${we}\:{have}\:\int\:\:\frac{{dt}}{{ct}^{\mathrm{2}} −{a}}\:=\int\:\:\frac{{dt}}{\left(\sqrt{{c}}{t}\right)^{\mathrm{2}} −\left(\sqrt{{a}}\right)^{\mathrm{2}} } \\ $$$$=\int\:\:\frac{{dt}}{\left(\sqrt{{c}}{t}−\sqrt{{a}}\right)\left(\sqrt{{c}}{t}+\sqrt{{a}}\right)} \\ $$$$=\int\:\left(\frac{\mathrm{1}}{\sqrt{{c}}{t}−\sqrt{{a}}}−\frac{\mathrm{1}}{\sqrt{{c}}{t}+\sqrt{{a}}}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{ac}}}{ln}\mid\frac{\sqrt{{c}}{t}−\sqrt{{a}}}{\sqrt{{c}}{t}\:+\sqrt{{a}}}\mid\:+{c} \\ $$$$\int\:\:\:\frac{{dt}}{\left({ct}^{\mathrm{2}} −{a}\right)^{\mathrm{2}} }\:=\int\:\frac{\mathrm{1}}{\left(\sqrt{{c}}{t}−\sqrt{{a}}\right)^{\mathrm{2}} \left(\sqrt{{c}}{t}+\sqrt{{a}}\right)^{\mathrm{2}} } \\ $$$${let}\:{decompose}\:{F}\left({t}\right)=\frac{\mathrm{1}}{\left(\sqrt{{c}}{t}−\sqrt{{a}}\right)^{\mathrm{2}} \left(\sqrt{{c}}{t}+\sqrt{{a}}\right)^{\mathrm{2}} } \\ $$$${F}\left({t}\right)=\frac{\alpha}{\sqrt{{c}}{t}\:−\sqrt{{a}}}\:+\frac{\beta}{\left(\sqrt{{c}}{t}−\sqrt{{a}}\right)^{\mathrm{2}} }\:+\frac{\lambda}{\sqrt{{c}}{t}+\sqrt{{a}}}\:+\frac{\rho}{\left(\sqrt{{c}}{t}+\sqrt{{a}}\right)^{\mathrm{2}} } \\ $$$$...{be}\:{continued}... \\ $$
